题目内容
13.在四边形ABCD中,若$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$,且|$\overrightarrow{AB}$|=|$\overrightarrow{AD}$|,则四边形ABCD为( )| A. | 矩形 | B. | 菱形 | ||
| C. | 正方形 | D. | 不是矩形、菱形的四边形 |
分析 由$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$,推出四边形ABCD是平行四边形,由|$\overrightarrow{AB}$|=|$\overrightarrow{AD}$|,推出AB=AD,推出四边形ABCD是菱形.
解答 解:∵$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$,
∴四边形ABCD是平行四边形,
∵|$\overrightarrow{AB}$|=|$\overrightarrow{AD}$|,
∴AB=AD,
∴四边形ABCD是菱形.
故选B.
点评 本题考查平面向量、平行四边形的判定和性质、菱形的判定和性质等知识,解题的关键是理解平面向量的平行四边形法则,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.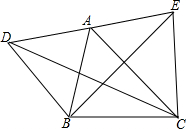 如图,A为DE的中点,设S1=S△DBC,S2=S△ABC,S3=S△EBC,则S1,S2,S3的关系是( )
如图,A为DE的中点,设S1=S△DBC,S2=S△ABC,S3=S△EBC,则S1,S2,S3的关系是( )
 如图,A为DE的中点,设S1=S△DBC,S2=S△ABC,S3=S△EBC,则S1,S2,S3的关系是( )
如图,A为DE的中点,设S1=S△DBC,S2=S△ABC,S3=S△EBC,则S1,S2,S3的关系是( )| A. | S2=$\frac{3}{2}$(S1+S3) | B. | S2=$\frac{1}{2}$(S3-S1) | C. | S2=$\frac{1}{2}$(S1+S3) | D. | S2=$\frac{3}{2}$(S3-S1) |
2.已知|x|=2,|y|=4,且x>y,则x-y的值为( )
| A. | 6 | B. | 6或2 | C. | ±6或±2 | D. | -2或-6 |
 如图,已知∠B=∠E,AB=DE,要推得△ABC≌△EDF,若以“AAS”为依据,缺条件∠ACB=∠DFE.
如图,已知∠B=∠E,AB=DE,要推得△ABC≌△EDF,若以“AAS”为依据,缺条件∠ACB=∠DFE. 如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE||BC,DE交AF于点G,设AD=5,AB=15,AC=12,GF=6.
如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE||BC,DE交AF于点G,设AD=5,AB=15,AC=12,GF=6.