题目内容
18.用加减法解下列方程组:(1)$\left\{\begin{array}{l}{4m-3n+1=0}\\{2m+6n=7}\end{array}\right.$
(2)$\left\{\begin{array}{l}{5x+2y=2}\\{7x-5y=34}\end{array}\right.$
(3)$\left\{\begin{array}{l}{3x+y+1=0}\\{3y=2x+19}\end{array}\right.$
(4)$\left\{\begin{array}{l}{3x-4y+5=0}\\{5x+2y=9}\end{array}\right.$
(5)$\left\{\begin{array}{l}{8x+3y+2=0}\\{6x+5y+7=0}\end{array}\right.$
(6)$\left\{\begin{array}{l}{\frac{x+1}{3}-\frac{y+2}{4}=0}\\{\frac{x-3}{4}-\frac{y-3}{3}=\frac{1}{12}}\end{array}\right.$.
分析 各方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{4m-3n=-1①}\\{2m+6n=7②}\end{array}\right.$,
①×2+②得:10m=5,即m=0.5,
把m=0.5代入①得:n=1,
则方程组的解为$\left\{\begin{array}{l}{m=0.5}\\{n=1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{5x+2y=2①}\\{7x-5y=34②}\end{array}\right.$,
①×5+②×2得:39x=78,即x=2,
把x=2代入①得:y=-4,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-4}\end{array}\right.$;
(3)方程组整理得:$\left\{\begin{array}{l}{3x+y=-1①}\\{2x-3y=-19②}\end{array}\right.$,
①×3+②得:11x=-22,即x=-2,
把x=-2代入①得:y=5,
则方程组的解为$\left\{\begin{array}{l}{x=-2}\\{y=5}\end{array}\right.$;
(4)$\left\{\begin{array}{l}{3x-4y=-5①}\\{5x+2y=9②}\end{array}\right.$,
①+②×2得:13x=13,即x=1,
把x=1代入①得:y=2,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$;
(5)方程组整理得:$\left\{\begin{array}{l}{8x+3y=-2①}\\{6x+5y=-7②}\end{array}\right.$,
①×5-②×3得:22x=11,即x=0.5,
把x=0.5代入①得:y=-2,
则方程组的解为$\left\{\begin{array}{l}{x=0.5}\\{y=-2}\end{array}\right.$;
(6)方程组整理得:$\left\{\begin{array}{l}{4x-3y=2①}\\{3x-4y=4②}\end{array}\right.$,
①×4-②×3得:7x=-5,即x=-$\frac{5}{7}$,
把x=-$\frac{5}{7}$代入①得:y=-$\frac{19}{21}$,
则方程组的解为$\left\{\begin{array}{l}{x=-\frac{5}{7}}\\{y=-\frac{19}{21}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

 如图,在△ABc中,D是Bc边的中点,且AD=AC,DE⊥BC,DE与AB交于点E,EC与AD交于点F
如图,在△ABc中,D是Bc边的中点,且AD=AC,DE⊥BC,DE与AB交于点E,EC与AD交于点F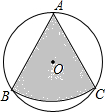 如图,从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,求圆锥的底面圆半径(结果保留π)
如图,从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,求圆锥的底面圆半径(结果保留π)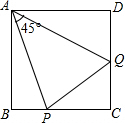 如图,在正方形ABCD中,P、Q分别为BC、CD边上的点,且∠PAQ=45°,△PCQ的周长为4,正方形ABCD的边长是多少?
如图,在正方形ABCD中,P、Q分别为BC、CD边上的点,且∠PAQ=45°,△PCQ的周长为4,正方形ABCD的边长是多少?