题目内容
12.解下列不等式和方程:(1)$\sqrt{5}$x>3$\sqrt{5}$x-4$\sqrt{3}$;
(2)$\frac{1}{3}$(2-$\sqrt{3}$x)=1-$\sqrt{12}$x.
分析 (1)利用不等式的性质求得x即可;
(2)利用解方程的步骤与方法求得答案即可.
解答 解:(1)$\sqrt{5}$x>3$\sqrt{5}$x-4$\sqrt{3}$
$\sqrt{5}$x-3$\sqrt{5}$x>-4$\sqrt{3}$
-2$\sqrt{5}$x>-4$\sqrt{3}$
x<$\frac{2}{5}$$\sqrt{15}$;
(2)$\frac{1}{3}$(2-$\sqrt{3}$x)=1-$\sqrt{12}$x
$\frac{2}{3}$-$\frac{\sqrt{3}}{3}$x=1-2$\sqrt{3}$x
2$\sqrt{3}$x-$\frac{\sqrt{3}}{3}$x=1-$\frac{2}{3}$
$\frac{5\sqrt{3}}{3}$x=$\frac{1}{3}$
x=$\frac{\sqrt{3}}{15}$.
点评 此题考查二次根式的实际运用,掌握解不等式与方程的步骤与方法是解决问题的关键.

练习册系列答案
相关题目
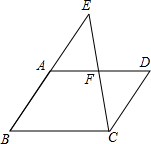 如图,在?ABCD中,点E在BA的延长线上,连结CE交AD于点F,且F是AD的中点,求证:AE=CD.
如图,在?ABCD中,点E在BA的延长线上,连结CE交AD于点F,且F是AD的中点,求证:AE=CD. 如图,∠1是△ABC的一个外角,∠2=∠BAC+∠BCA,∠1+∠2+∠3=360°.
如图,∠1是△ABC的一个外角,∠2=∠BAC+∠BCA,∠1+∠2+∠3=360°. 如图,某同学在完成数学作业时,遇到了这样一个问题,AB=CD,BC=AD.求证:∠A=∠C.
如图,某同学在完成数学作业时,遇到了这样一个问题,AB=CD,BC=AD.求证:∠A=∠C. 如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E,求证:
如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E,求证: