题目内容
2.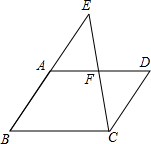 如图,在?ABCD中,点E在BA的延长线上,连结CE交AD于点F,且F是AD的中点,求证:AE=CD.
如图,在?ABCD中,点E在BA的延长线上,连结CE交AD于点F,且F是AD的中点,求证:AE=CD.
分析 由平行四边形的性质得出AB∥CD,得出∠EAF=∠D,由ASA证明△AEF≌△DCF,得出对应边相等即可.
解答 证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EAF=∠D,
又∵F是AD的中点,
∵AF=DF,
在△AEF和△DCF中,$\left\{\begin{array}{l}{∠EAF=∠D}&{\;}\\{AF=DF}&{\;}\\{∠AFE=∠DFC}&{\;}\end{array}\right.$,
∴△AEF≌△DCF(ASA)
∴AE=CD.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
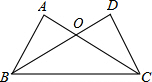 如图,在△ABC和△DCB中,AC与BD相交于点O,AB=DC,AC=BD.
如图,在△ABC和△DCB中,AC与BD相交于点O,AB=DC,AC=BD. 如图,在Rt△ABC中,∠C=90°,CD是斜边上的高,已知AD=2.8cm,BD=1.4cm,试求高CD的长(精确到0.01cm)
如图,在Rt△ABC中,∠C=90°,CD是斜边上的高,已知AD=2.8cm,BD=1.4cm,试求高CD的长(精确到0.01cm) 请用含字母a,b的式子表示如图所示图形阴影部分的面积,并求当a=4,b=3时阴影部分的面积.
请用含字母a,b的式子表示如图所示图形阴影部分的面积,并求当a=4,b=3时阴影部分的面积.