题目内容
7. 如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E,求证:
如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E,求证:(1)△BCA≌△DCE;
(2)BC=DC.
分析 先求出∠ACB=∠ECD,再利用“ASA”证明△ABC≌△EDC,然后根据“全等三角形对应角相等”证得结论.
解答 证明:∵∠BCE=∠DCA,
∴∠BCE+∠ECA=∠DCA+∠ECA,
即∠BCA=∠DCE.
在△ABC和△EDC中,
$\left\{\begin{array}{l}{∠A=∠E}\\{AC=EC}\\{∠BCA=∠DCE}\end{array}\right.$,
∴△ABC≌△EDC(ASA),
∴BC=DC.
点评 本题考查了全等三角形的判定与性质.求出相等的角∠ACB=∠ECD是解题的关键.

练习册系列答案
相关题目
18. 如图,用平面去截圆柱,截面形状是( )
如图,用平面去截圆柱,截面形状是( )
 如图,用平面去截圆柱,截面形状是( )
如图,用平面去截圆柱,截面形状是( )| A. |  | B. |  | C. |  | D. |  |
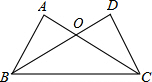 如图,在△ABC和△DCB中,AC与BD相交于点O,AB=DC,AC=BD.
如图,在△ABC和△DCB中,AC与BD相交于点O,AB=DC,AC=BD. 如图,有一块等腰直角三角形的绿地,面积为18平方千米,甲乙两人分别从顶点C、A同时骑摩托车出发,甲由C向B运动,速度为1千米/分,乙由A向C运动,速度是2千米/分,则$\frac{1}{2}$或$\frac{14}{5}$分钟后,两人相距2$\sqrt{2}$千米.
如图,有一块等腰直角三角形的绿地,面积为18平方千米,甲乙两人分别从顶点C、A同时骑摩托车出发,甲由C向B运动,速度为1千米/分,乙由A向C运动,速度是2千米/分,则$\frac{1}{2}$或$\frac{14}{5}$分钟后,两人相距2$\sqrt{2}$千米. 己知:在△ABC中,AD是BC边上的高,AD=BD,BE=AC,延长BE交AC于F,求证:BF是△ABC中AC边上的高.
己知:在△ABC中,AD是BC边上的高,AD=BD,BE=AC,延长BE交AC于F,求证:BF是△ABC中AC边上的高. 如图,∠A=50°,∠1=20°,∠2=25°,求∠BDC的度数.
如图,∠A=50°,∠1=20°,∠2=25°,求∠BDC的度数. 已知有理数a在数轴上的位置如图所示,把a,a的相反数,a的倒数,a的绝对值,a的负倒数按从小到大的顺序用“<”连接起来.
已知有理数a在数轴上的位置如图所示,把a,a的相反数,a的倒数,a的绝对值,a的负倒数按从小到大的顺序用“<”连接起来.