题目内容
9.下表记录了一名球员在罚球线上投篮的结果,| 投篮次数(n) | 50 | 100 | 150 | 209 | 250 | 300 | 350 |
| 投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 175 |
| 投中频率(n/m) | 0.56 | 0.60 | 0.52 | 0.50 | 0.49 | 0.51 | 0.58 |
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?
分析 (1)用投中的次数除以投篮的次数即可得出答案;
(2)计算出所有投篮的次数,再计算出总的命中数,继而可估计出这名球员投篮一次,投中的概率.
解答 解:(1)根据题意得:
78÷150=0.52;
104÷209≈0.50;
152÷300≈0.51;
175÷350≈0.58;
填表如下:
| 投篮次数(n) | 50 | 100 | 150 | 209 | 250 | 300 | 350 |
| 投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 175 |
| 投中频率(n/m) | 0.56 | 0.60 | 0.52 | 0.50 | 0.49 | 0.51 | 0.58 |
(2)由题意得:
投篮的总次数是50+100+150+209+250+300+350=1409(次),
投中的总次数是28+60+78+104+123+152+175=720(次),
则这名球员投篮的次数为1409次,投中的次数为720,
故这名球员投篮一次,投中的概率约为:$\frac{720}{1409}$≈0.5.
故答案为:0.5
点评 此题考查了利用频率估计概率的知识,注意这种概率的得出是在大量实验的基础上得出的,不能单纯的依靠几次决定.

练习册系列答案
相关题目
4.下列命题中,假命题是( )
| A. | 对角线互相垂直平分的四边形是矩形 | |
| B. | 邻角相等的菱形是正方形 | |
| C. | 对角线相等的菱形是正方形 | |
| D. | 一组邻边相等的平行四边形是菱形 |
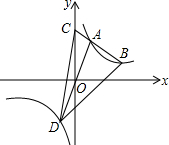 如图,已知直线y=-x+5交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交y轴于C点,AO的延长线交双曲线y=$\frac{k}{x}$(x<0)于D点,且S△BCD=15,则k=6.
如图,已知直线y=-x+5交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交y轴于C点,AO的延长线交双曲线y=$\frac{k}{x}$(x<0)于D点,且S△BCD=15,则k=6.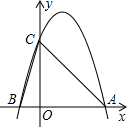 如图所示,二次函数y=-2x2+4x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
如图所示,二次函数y=-2x2+4x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C. (1)解方程组$\left\{\begin{array}{l}3x+4y=19\\ x-4y=1\end{array}\right.$
(1)解方程组$\left\{\begin{array}{l}3x+4y=19\\ x-4y=1\end{array}\right.$