(1)解方程组$\left\{\begin{array}{l}3x+4y=19\\ x-4y=1\end{array}\right.$(2)解不等式:$\frac{1+2x}{3}$≥x-1.并把解集在数轴上表示出来．题目和参考答案——青夏教育精英家教网—

题目内容

1．

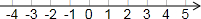（1）解方程组$\left\{\begin{array}{l}3x+4y=19\\ x-4y=1\end{array}\right.$
（2）解不等式：$\frac{1+2x}{3}$≥x-1，并把解集在数轴上表示出来．

分析（1）方程组利用加减消元法求出解即可；
（2）不等式去分母，去括号，移项合并，把x系数化为1，求出解集，表示在数轴上即可．

解答解：（1）$\left\{\begin{array}{l}{3x+4y=19①}\\{x-4y=1②}\end{array}\right.$，
①+②得：4x=20，即x=5，
将x=5代入方程②得：y=1，
∴原方程组的解为$\left\{\begin{array}{l}x=5\\ y=1\end{array}\right.$；
（2）去分母得：1+2x≥3x-3，
移项合并得：-x≥-4，
解得：x≤4，

点评此题考查了解二元一次方程组，解一元一次不等式，熟练掌握运算法则是解本题的关键．

练习册系列答案

相关题目

11．

在四边形ABCD中，对角线AC与BD交于点O，△ABO≌△CDO．若∠ABO=∠DCO，求证：四边形ABCD为矩形．

12．解方程组$\left\{\begin{array}{l}{ax+by=2}\\{cx-7y=8}\end{array}\right.$时，一学生把c看错而得$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$，而正确的解是$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$，那么a=4，b=5，c=-2．

9．下表记录了一名球员在罚球线上投篮的结果，

投篮次数（n）	50	100	150	209	250	300	350
投中次数（m）	28	60	78	104	123	152	175
投中频率（n/m）	0.56	0.60	0.52	0.50	0.49	0.51	0.58

（1）计算并填写表中的投中频率（精确到0.01）；
（2）这名球员投篮一次，投中的概率约是多少（精确到0.1）？

16．已知A点的坐标为（n+3，3），B点的坐标为（n-4，n），AB∥x轴，则线段AB的长为（　　）

	A．	如果两个角相等，则它们是对顶角
	B．	实数包括有理数、无理数
	C．	两直线被第三直线所截，内错角相等
	D．	若a²=b²，则a=b

13．计算
（1）3$\sqrt{2}$+2$\sqrt{2}$
（2）$\root{3}{-8}$-$\sqrt{4}$+$\sqrt{0.04}$．

10．先化简，再求值：[（xy+2）（xy-2）-2x²y²+4]，其中x=10，y=-$\frac{1}{25}$．

15．如图，
（1）△ABC是斜边AB的长为3的等腰直角三角形，在△ABC内作第1个内接正方形A₁B₁D₁E₁（D₁、E₁在AB上，A₁、B₁分别在AC、BC上），再在△A₁B₁C内用同样的方法作第2个内接正方形A₂B₂D₂E₂，…如此下去，操作n次，则第一个内接正方形的边长是1，第n个小正方形A_nB_nD_nE_n 的边长是$\frac{1}{{3}^{（n-1）}}$．
（2）在△ABC中，BC=12，高AD=8，四边形PQMN为△ABC的内接矩形，（P在AB上，Q在AC上，M、N在BC上），
①求当PQ为何值时，矩形PQMN面积最大．
②若再在△APQ中作一个内接矩形P₂Q₂M₂N₂，如此下去，操作n次，求PnQn的长．（直接写出结果）
（3）解完上述两题，根据其中一题你还能归纳出怎样的数学结论，请简单的写出一条．

试题分类