题目内容
3．我们知道在一元二次方程x2=-1中，由于-1＜0，因而原方程无实数根．我们定义：i2=-1，我们把i称为虚数单位，当b≠0，把a+bi（其中a，b为实数）称为虚数．虚数的乘法法则：$\begin{array}{l}（{a+bi}）（{c+di}）\\=a•c+a•di+bi•c+bi•di\\=ac+ad•i+bc•i+bd•{i^2}\\=ac+（{ad+bc}）i+bd•（{-1}）\\=（{ac-bd}）+（{ad+bc}）i\end{array}$
则式子 $（{1+\sqrt{3}i}）（{1-\sqrt{3}i}）$=4．
分析 阅读理解题，根据提供的公式代入计算．
解答 解：$（{1+\sqrt{3}i}）（{1-\sqrt{3}i}）$=12-（$\sqrt{3}$i）2=1-3i2，
∵i2=-1，
∴$（{1+\sqrt{3}i}）（{1-\sqrt{3}i}）$=1-3×（-1）=1+3=4．
点评 本题考查了阅读理解能力，平方差公式的运用和整体代入思想．
练习册系列答案
阅读快车系列答案
相关题目
9．下表记录了一名球员在罚球线上投篮的结果，
（1）计算并填写表中的投中频率（精确到0.01）；
（2）这名球员投篮一次，投中的概率约是多少（精确到0.1）？
| 投篮次数（n） | 50 | 100 | 150 | 209 | 250 | 300 | 350 |
| 投中次数（m） | 28 | 60 | 78 | 104 | 123 | 152 | 175 |
| 投中频率（n/m） | 0.56 | 0.60 | 0.52 | 0.50 | 0.49 | 0.51 | 0.58 |
（2）这名球员投篮一次，投中的概率约是多少（精确到0.1）？
7．
如图．已知AB∥EF，∠BAE的平分线交EF于点C，∠E=64°，则∠ACE的度数为（ ）
如图．已知AB∥EF，∠BAE的平分线交EF于点C，∠E=64°，则∠ACE的度数为（ ）| A． | 54° | B． | 58° | C． | 60° | D． | 64° |
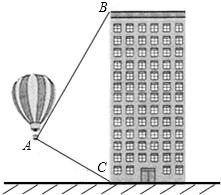小明和小华准备利用迷你热气球来测量如图所示的高楼BC的高度，从热气球探测到此高楼顶部的仰角为66°，此高楼底部的俯角为36°，此时热气球距离C的距离是42米，请计算这栋高楼的高度是多少米（sin66°≈0.90，cos66°≈0.40，tan66°≈2.25，sin36°≈0.60，cos36°≈0.80，tan36°≈0.75）
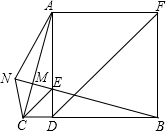如图，已知正方形ADBF，点E在AD上，且∠AEB=105°，EC∥DF交BD的延长线于C，N为BE延长线上一点，BN交AC于M，且CE=2MN，连结AN、CN，下列结论：