题目内容
14.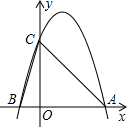 如图所示,二次函数y=-2x2+4x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
如图所示,二次函数y=-2x2+4x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.(1)求m的值及点B的坐标;
(2)求△ABC的面积;
(3)该二次函数图象上有一点D(x,y),使S△ABD=S△ABC,请求出D点的坐标.
分析 (1)先把点A坐标代入解析式,求出m的值,进而求出点B的坐标;
(2)根据二次函数的解析式求出点C的坐标,进而求出△ABC的面积;
(3)根据S△ABD=S△ABC求出点D纵坐标的绝对值,然后分类讨论,求出点D的坐标.
解答 解:(1)∵函数过A(3,0),
∴-18+12+m=0,
∴m=6,
∴该函数解析式为:y=-2x2+4x+6,
∴当-2x2+4x+6=0时,x1=-1,x2=3,
∴点B的坐标为(-1,0);
(2)C点坐标为(0,6),${S_{△ABC}}=\frac{4×6}{2}=12$;
(3)∵S△ABD=S△ABC=12,
∴S△ABD=$\frac{4×|h|}{2}$=12,
∴|h|=6,
①当h=6时:-2x2+4x+6=6,解得:x1=0,x2=2
∴D点坐标为(0,6)或(2,6),
②当h=-6时:-2x2+4x+6=-6,解得:x1=1+$\sqrt{7}$,x2=1-$\sqrt{7}$
∴D点坐标为(1+$\sqrt{7}$,-6)、(1-$\sqrt{7}$,-6)
∴D点坐标为(0,6)、(2,6)、(1+$\sqrt{7}$,-6)、(1-$\sqrt{7}$,-6).
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键是熟练掌握二次函数的性质,解答(3)问需要分类讨论,此题难度一般.

练习册系列答案
相关题目
2.衣柜不透明的盒子中有3个红球和2个白球,它们除颜色外都相同,若从中任何摸出一个球,则下列叙述正确的是( )
| A. | 摸到红球是必然事件 | B. | 摸到黑球与摸到白球是随机事件 | ||
| C. | 摸到红球比摸到白球的可能性大 | D. | 摸到白球比摸到红球的可能性大 |
9.下表记录了一名球员在罚球线上投篮的结果,
(1)计算并填写表中的投中频率(精确到0.01);
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?
| 投篮次数(n) | 50 | 100 | 150 | 209 | 250 | 300 | 350 |
| 投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 175 |
| 投中频率(n/m) | 0.56 | 0.60 | 0.52 | 0.50 | 0.49 | 0.51 | 0.58 |
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?
6.下列命题中正确的是( )
| A. | 如果两个角相等,则它们是对顶角 | |
| B. | 实数包括有理数、无理数 | |
| C. | 两直线被第三直线所截,内错角相等 | |
| D. | 若a2=b2,则a=b |

 如图是一个汉字“互”字,其中,GH∥EF,∠1=∠2,∠MEF=∠GHN.求证:
如图是一个汉字“互”字,其中,GH∥EF,∠1=∠2,∠MEF=∠GHN.求证: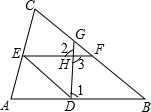 完成下面的证明过程
完成下面的证明过程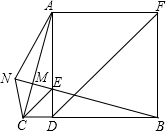 如图,已知正方形ADBF,点E在AD上,且∠AEB=105°,EC∥DF交BD的延长线于C,N为BE延长线上一点,BN交AC于M,且CE=2MN,连结AN、CN,下列结论:
如图,已知正方形ADBF,点E在AD上,且∠AEB=105°,EC∥DF交BD的延长线于C,N为BE延长线上一点,BN交AC于M,且CE=2MN,连结AN、CN,下列结论: