题目内容
9.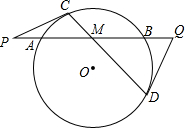 AB是⊙O的一条弦,它的中点为M,过点M作一条非直径的弦CD,过点C和D作⊙O的两条切线,分别与直线AB相交于P、Q两点.求证:PA=QB.
AB是⊙O的一条弦,它的中点为M,过点M作一条非直径的弦CD,过点C和D作⊙O的两条切线,分别与直线AB相交于P、Q两点.求证:PA=QB.
分析 连接OM、OP、OQ、OC、OD,如图,根据切线的性质可得∠PCO=∠QDO=90°,根据垂径定理的推论可得OM⊥AB即∠PMO=∠QMO=90°,从而可得∠PCO=∠PMO,∠QDO+∠QMO=180°,即可得到P、C、M、O四点共圆,Q、D、O、M四点共圆,根据圆周角定理可得∠OPM=∠OCM,∠ODM=∠OQM.由OC=OD可得∠OCD=∠ODC,从而可得∠OPM=∠OQM,根据等角对等边可得OP=OQ,根据等腰三角形的性质(三线合一)可得MP=MQ,结合条件MA=MB,就可得到PA=QB.
解答 证明:连接OM、OP、OQ、OC、OD,如图所示.
∵PC、DQ为⊙O的切线,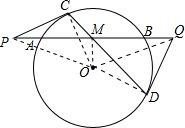 M为AB的中点,
M为AB的中点,
∴∠PCO=∠QDO=90°,OM⊥AB即∠PMO=∠QMO=90°,
∴∠PCO=∠PMO,∠QDO+∠QMO=180°,
∴P、C、M、O四点共圆,Q、D、O、M四点共圆,
∴∠OPM=∠OCM,∠ODM=∠OQM.
∵OC=OD,∴∠OCD=∠ODC,
∴∠OPM=∠OQM,
∴OP=OQ.
∵OM⊥PQ,∴MP=MQ.
∵MA=MB,∴PA=QB.
点评 本题主要考查了切线的性质、垂径定理的推论、四点共圆的判定、圆周角定理、等腰三角形的判定与性质等知识,证到P、C、M、O四点共圆及Q、D、O、M四点共圆,是解决本题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
4.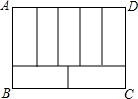 如图,周长为34cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为( )
如图,周长为34cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为( )
 如图,周长为34cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为( )
如图,周长为34cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为( )| A. | 49cm2 | B. | 74cm2 | C. | 68cm2 | D. | 70cm2 |
19.用配方法将x2-2x-2=0变形,正确的是( )
| A. | (x-1)2=1 | B. | (x+1)2=3 | C. | (x-1)2=3 | D. | (x+1)2=1 |
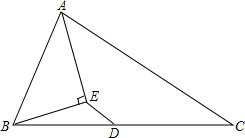 如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E,若AB=5,AC=7,求ED.
如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E,若AB=5,AC=7,求ED.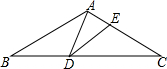 如图,等腰△ABC的腰长为2$\sqrt{3}$,D为底边BC上一点,且BD=2,E为腰AC上一点,若∠ADE=∠B=30°,则CE的长为$\frac{4\sqrt{3}}{3}$.
如图,等腰△ABC的腰长为2$\sqrt{3}$,D为底边BC上一点,且BD=2,E为腰AC上一点,若∠ADE=∠B=30°,则CE的长为$\frac{4\sqrt{3}}{3}$.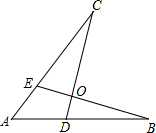 如图.下面四个条件中,请你选出三个,以其中两个为已知条件,另一个为求证,编一道题并证明(只需写出一种情况).①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.
如图.下面四个条件中,请你选出三个,以其中两个为已知条件,另一个为求证,编一道题并证明(只需写出一种情况).①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.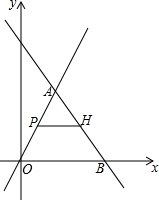 如图,在平面直角坐标系中,直线y=2x上有一点A,点A的横坐标为2,直线y=kx+b经过点A与x轴正半轴交于点B.△AOB的面积为10,点P是线段OA上一动点,过点P作PH∥x轴交线段AB于H,点P的纵坐标为m.
如图,在平面直角坐标系中,直线y=2x上有一点A,点A的横坐标为2,直线y=kx+b经过点A与x轴正半轴交于点B.△AOB的面积为10,点P是线段OA上一动点,过点P作PH∥x轴交线段AB于H,点P的纵坐标为m.