题目内容
18.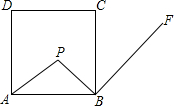 如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )
如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )| A. | 2或$\frac{25}{2}$ | B. | 2 | C. | $\frac{25}{2}$ | D. | 2或$\frac{15}{2}$ |
分析 由正方形的性质得出AB=BC=5,证出∠ABP=∠CBF,分两种情况:当△ABP∽△MBC时,$\frac{BM}{AB}$=$\frac{BC}{BP}$;当△ABP∽△CBM时,$\frac{BM}{BP}$=$\frac{CB}{AB}$;分别求出BM的长即可.
解答 解:∵正方形ABCD的边长为5,
∴AB=BC=5,
∵∠ABC=∠FBP=90°,
∴∠ABP=∠CBF,
当△ABP∽△MBC时,$\frac{BM}{AB}$=$\frac{BC}{BP}$,
∴BM=5×5÷2=$\frac{25}{2}$;
当△ABP∽△CBM时,$\frac{BM}{BP}$=$\frac{CB}{AB}$,
∴BM=5×2÷5=2,
故选A.
点评 本题考查了正方形的性质、相似三角形的判定与性质;熟练掌握正方形的性质,证明三角形相似是解决问题的关键.

练习册系列答案
相关题目
 △ABC内接于⊙O,∠B=60°,AC=2cm,⊙O的直径为多少?
△ABC内接于⊙O,∠B=60°,AC=2cm,⊙O的直径为多少? 如图,△ABC内接于⊙O,∠B=30°,AC=2cm,求⊙O的半径.
如图,△ABC内接于⊙O,∠B=30°,AC=2cm,求⊙O的半径.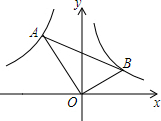 如图,Rt△AOB中,∠AOB=90°,点A在双曲线y=$\frac{k}{x}$(x<0)上,点B在双曲线y=$\frac{1}{x}$(x>0)上.
如图,Rt△AOB中,∠AOB=90°,点A在双曲线y=$\frac{k}{x}$(x<0)上,点B在双曲线y=$\frac{1}{x}$(x>0)上.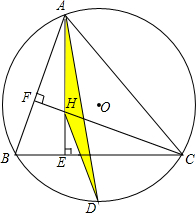 已知,△ABC内接于⊙O,∠BAC=60°,AE⊥BC,CF⊥AB.AE,CF相交于点H,点D为弧BC的中点,连接HD,AD.求证:△AHD为等腰三角形.
已知,△ABC内接于⊙O,∠BAC=60°,AE⊥BC,CF⊥AB.AE,CF相交于点H,点D为弧BC的中点,连接HD,AD.求证:△AHD为等腰三角形.