题目内容
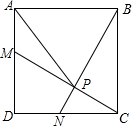 如图,在正方形ABCD中,M、N分别为AD,DC的中点,MC与NB交于点P,求证:PA=AB.
如图,在正方形ABCD中,M、N分别为AD,DC的中点,MC与NB交于点P,求证:PA=AB.考点:正方形的性质,全等三角形的判定与性质,三角形中位线定理
专题:证明题
分析:延长CM交BA延长线于E,通过证明△BCN≌△CDM,所以∠CBN=∠DCM,所以∠DCM+∠BNC=90°,∠CPN=90°又因为A是RT△BPE斜边BE中点,进而证明AP=AB.
解答: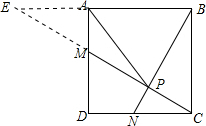 证明:延长CM交BA延长线于E,
证明:延长CM交BA延长线于E,
∵M为中点,AB∥CD,
∴AE=CD=AB,
∴A是BE中点,
在△BCN与△CDM中,
,
∴△BCN≌△CDM(SAS),
∴∠CBN=∠DCM,
∴∠DCM+∠BNC=90°,∠CPN=90°
又∵A是RT△BPE斜边BE中点,
∴AP=AB.
 证明:延长CM交BA延长线于E,
证明:延长CM交BA延长线于E,∵M为中点,AB∥CD,
∴AE=CD=AB,
∴A是BE中点,
在△BCN与△CDM中,
|
∴△BCN≌△CDM(SAS),
∴∠CBN=∠DCM,
∴∠DCM+∠BNC=90°,∠CPN=90°
又∵A是RT△BPE斜边BE中点,
∴AP=AB.
点评:本题考查了正方形的性质、全等三角形的判定和性质,题目的综合性较强,解题的关键是正确的作出辅助线,各种全等三角形.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目

 如图,将Rt△ABC纸片沿BD折叠后,C与AB中点E重合,CD=4,则AD=
如图,将Rt△ABC纸片沿BD折叠后,C与AB中点E重合,CD=4,则AD= 如图,等边△ABC中,点D、E、F分别在边BC、CA、AB上,且BD=2DC,CE=2EA,AF=2FB,AD与BE相交于点P,BE与CF相交于点Q,CF与AD相交于点R,则AP:PR:RD=
如图,等边△ABC中,点D、E、F分别在边BC、CA、AB上,且BD=2DC,CE=2EA,AF=2FB,AD与BE相交于点P,BE与CF相交于点Q,CF与AD相交于点R,则AP:PR:RD= 如图,已知AB为圆O的弦,直径MN与AB相交于圆O内,MC⊥AB于C,ND⊥AB于D.求证:AC=BD,OC=OD.
如图,已知AB为圆O的弦,直径MN与AB相交于圆O内,MC⊥AB于C,ND⊥AB于D.求证:AC=BD,OC=OD. 如图,等边△ABC中,点D为BC边的中点,∠BEC=120°,连接AE、DE,求证:AE=2DE.
如图,等边△ABC中,点D为BC边的中点,∠BEC=120°,连接AE、DE,求证:AE=2DE. 计算题:
计算题: