题目内容
 如图,已知AB为圆O的弦,直径MN与AB相交于圆O内,MC⊥AB于C,ND⊥AB于D.求证:AC=BD,OC=OD.
如图,已知AB为圆O的弦,直径MN与AB相交于圆O内,MC⊥AB于C,ND⊥AB于D.求证:AC=BD,OC=OD.考点:全等三角形的判定与性质,勾股定理,垂径定理
专题:证明题
分析:根据垂径定理,可得EA与EB的关系,根据三角形的中位线,可得CF与FN的关系,再根据三角形的中位线,可得EC与ED的关系,根据等式的性质,可得AC与BD的关系;根据全等三角形的判定与性质,可得OC与OD的关系.
解答: 证明:连接CN,作OE⊥AB于E,交CN于点F,
证明:连接CN,作OE⊥AB于E,交CN于点F,
∵OE⊥AB,
∴EA=EB.
∵MC⊥AB,ND⊥AB,OE⊥AB,
∴MC‖OE‖ND.
∵OM=ON,
∴CF=FN.
∵EF∥DN,CF=FN,
∴EC=ED.
∵EA-EC=EB-ED
∴AC=BD;
在△ECO和△EDO中,
,
∴△ECO≌△EDO(SAS),
∴OC=OD.
 证明:连接CN,作OE⊥AB于E,交CN于点F,
证明:连接CN,作OE⊥AB于E,交CN于点F,∵OE⊥AB,
∴EA=EB.
∵MC⊥AB,ND⊥AB,OE⊥AB,
∴MC‖OE‖ND.
∵OM=ON,
∴CF=FN.
∵EF∥DN,CF=FN,
∴EC=ED.
∵EA-EC=EB-ED
∴AC=BD;
在△ECO和△EDO中,
|
∴△ECO≌△EDO(SAS),
∴OC=OD.
点评:本题考查了全等三角形的判定与性质,利用三角形的中位线是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数轴上不小于-4的非正整数有( )
| A、5 | B、4 | C、3 | D、2 |
绝对值不大于3的整数的积是( )
| A、4 | B、-4 | C、0 | D、12 |
已知y=-1是方程my=y+2的解,求m2-2m+1的值( )
| A、3 | B、4 | C、-1 | D、-3 |
 如图,在?ABCD中,∠A+∠C=140°,将?ABCD折叠,使点D、C分别落在点F、E处(点F、E都在AB所在的直线上),折痕为MN,则∠AMF等于
如图,在?ABCD中,∠A+∠C=140°,将?ABCD折叠,使点D、C分别落在点F、E处(点F、E都在AB所在的直线上),折痕为MN,则∠AMF等于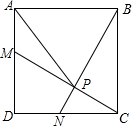 如图,在正方形ABCD中,M、N分别为AD,DC的中点,MC与NB交于点P,求证:PA=AB.
如图,在正方形ABCD中,M、N分别为AD,DC的中点,MC与NB交于点P,求证:PA=AB.