题目内容
 如图,等边△ABC中,点D为BC边的中点,∠BEC=120°,连接AE、DE,求证:AE=2DE.
如图,等边△ABC中,点D为BC边的中点,∠BEC=120°,连接AE、DE,求证:AE=2DE.考点:全等三角形的判定与性质,等边三角形的判定与性质,旋转的性质
专题:证明题
分析:根据旋转的性质,可得△ABE≌△ACF,且△AEF为等边三角形,根据三角形外角的性质,可得∠EBA+∠ACE=120°-(∠EAB+∠EAC)=60°,根据全等三角形的判定与性质,可得EB=DG,∠EBD=∠GCD,再根据全等三角形的判定与性质,可得EG=EF,根据等量代换,可得答案.
解答:证明:如图:

将△ABE绕点A逆时针旋转60°得到△ACF,连接EF.延长ED至点G,
使DG=ED,连接CG.
∴△ABE≌△ACF,且△AEF为等边三角形.
∴AE=AF=EF,BE=CF,∠FCA=∠EBA
∵∠EBA+∠ACE=120°-(∠EAB+∠EAC)=60°
∴∠FCE=∠EBA+∠ACE=60°.
在△EBD和△GCD中,
,
∴△EBD≌△GCD (SAS),
∴EB=DG,∠EBD=∠GCD,
∴CG=CF,∠GCE=∠GCD+∠ECD=∠EBC+∠ECB=60°=∠FCE.
在△ECG和△ECF中,
,
∴△ECG≌△ECF(SAS)
∴EG=EF,
∴EF=EG=2ED,
∴AE=2ED.

将△ABE绕点A逆时针旋转60°得到△ACF,连接EF.延长ED至点G,
使DG=ED,连接CG.
∴△ABE≌△ACF,且△AEF为等边三角形.
∴AE=AF=EF,BE=CF,∠FCA=∠EBA
∵∠EBA+∠ACE=120°-(∠EAB+∠EAC)=60°
∴∠FCE=∠EBA+∠ACE=60°.
在△EBD和△GCD中,
|
∴△EBD≌△GCD (SAS),
∴EB=DG,∠EBD=∠GCD,
∴CG=CF,∠GCE=∠GCD+∠ECD=∠EBC+∠ECB=60°=∠FCE.
在△ECG和△ECF中,
|
∴△ECG≌△ECF(SAS)
∴EG=EF,
∴EF=EG=2ED,
∴AE=2ED.
点评:本题考查了全等三角形的判定与性质,利用了旋转的性质,全等三角形的判定与性质,构造全等三角形是解题关键.

练习册系列答案
相关题目
已知y=-1是方程my=y+2的解,求m2-2m+1的值( )
| A、3 | B、4 | C、-1 | D、-3 |
已知多项式3x2-x3+5x4-7+23x,将该多项式按降幂排列( )
| A、3x2-x3+5x4-7+23x |
| B、5x4+23x+3x2-x3-7 |
| C、5x4-x3+3x2+23x-7 |
| D、-x3+5x4+3x2-7+23x |
下列方程组中是二元一次方程组的是( )
A、
| |||||||||
B、
| |||||||||
C、
| |||||||||
D、
|
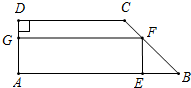 在直角梯形ABCD中,AB∥DC,∠A=90°,AB=6,CD=4,AD=2,作梯形的内接矩形AEFG,使点E在AB上,点F在BC上,点G在AD上.设EF=x.
在直角梯形ABCD中,AB∥DC,∠A=90°,AB=6,CD=4,AD=2,作梯形的内接矩形AEFG,使点E在AB上,点F在BC上,点G在AD上.设EF=x.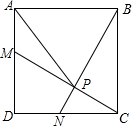 如图,在正方形ABCD中,M、N分别为AD,DC的中点,MC与NB交于点P,求证:PA=AB.
如图,在正方形ABCD中,M、N分别为AD,DC的中点,MC与NB交于点P,求证:PA=AB.