题目内容
18.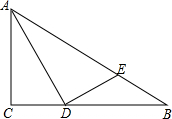 已知,如图,在Rt△ABC中,∠ACB=90°,AB=4,AD是∠BAC的平分线,过点D作DE⊥AD,垂足为点D,交AB于点E,且$\frac{BE}{AB}=\frac{1}{4}$.
已知,如图,在Rt△ABC中,∠ACB=90°,AB=4,AD是∠BAC的平分线,过点D作DE⊥AD,垂足为点D,交AB于点E,且$\frac{BE}{AB}=\frac{1}{4}$.(1)求线段BD的长;
(2)求∠ADC的正切值.
分析 (1)根据余角的性质得到∠CAD=∠DAB,推出∠BAD=∠BDE,得到△BED∽△BDA,由相似三角形的性质得到BD2=BE•BA,即可得到结论;
(2)由余角的性质得到∠ADE=∠AED,根据余角的性质得到$\frac{AD}{AE}=\frac{AB}{BD}$,根据三角形函数的定义即可得到结论.
解答 解:(1)∵DE⊥AD,
∴∠BDE=∠CAD=90°-∠CDA,
∵∠CAD=∠DAB,
∴∠BAD=∠BDE,
∵∠B=∠B,
∴△BED∽△BDA,
∴BD2=BE•BA,
∵AB=4,$\frac{BE}{AB}=\frac{1}{4}$,
∴BE=1,
∴BD2=1×4=4,
∴BD=2;
(2)∵DE⊥AD,
∴∠ADE=∠C=90°,
∵∠CAD=∠DAB,
∵△ACD∽△ADE,
∴$\frac{AC}{CD}=\frac{AD}{DE}$,
∵△BED∽△BDA,
∴$\frac{AD}{DE}=\frac{AB}{BD}$=$\frac{1}{2}$,
∴tan∠ADC=tan∠AED=$\frac{AD}{DE}$=2.
点评 本题考查了相似三角形的判定和性质,三角函数的定义,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用了这两种货车的情况如表所示;现用该公司3辆甲种货车和5辆乙种货车一次刚好运完这批货.
(1)问甲、乙两种货车每辆一次分别可运货多少吨?
(2)如果按每吨付费30元计算,货主应付运费多少元?
| 第一次 | 第二次 | |
| 甲种货车辆数(单位;辆) | 2 | 5 |
| 乙种货车辆数(单位:辆) | 3 | 6 |
| 累计运货吨数(单位:吨) | 15.5 | 35 |
(2)如果按每吨付费30元计算,货主应付运费多少元?
3.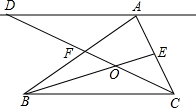 如图,△ABC的中线BE、CF交于点O,直线AD∥BC,与CF的延长线交于点D,则S△AFD:S四边形AFOE为( )
如图,△ABC的中线BE、CF交于点O,直线AD∥BC,与CF的延长线交于点D,则S△AFD:S四边形AFOE为( )
 如图,△ABC的中线BE、CF交于点O,直线AD∥BC,与CF的延长线交于点D,则S△AFD:S四边形AFOE为( )
如图,△ABC的中线BE、CF交于点O,直线AD∥BC,与CF的延长线交于点D,则S△AFD:S四边形AFOE为( )| A. | 1:2 | B. | 2:1 | C. | 2:3 | D. | 3:2 |
7.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
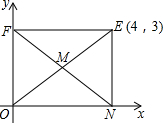 如图,矩形ONEF的对角线交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为(2,1.5).
如图,矩形ONEF的对角线交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为(2,1.5).