题目内容
3.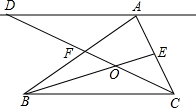 如图,△ABC的中线BE、CF交于点O,直线AD∥BC,与CF的延长线交于点D,则S△AFD:S四边形AFOE为( )
如图,△ABC的中线BE、CF交于点O,直线AD∥BC,与CF的延长线交于点D,则S△AFD:S四边形AFOE为( )| A. | 1:2 | B. | 2:1 | C. | 2:3 | D. | 3:2 |
分析 设△OEC的面积为s,求出△ADF的面积和四边形AFOE的面积即可求解.
解答 解:如图连接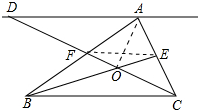 EF、AO,设△OEC的面积为s,
EF、AO,设△OEC的面积为s,
∵AF=BF,AE=EC,
∴EF∥BC,EF=$\frac{1}{2}$BC,
∴$\frac{EF}{BC}=\frac{FO}{OC}=\frac{1}{2}$,
∴S△EOC=S△AOE=s,${S}_{△AOF}={\frac{1}{2}S}_{△AOC}$=s,
∴S△AFC=3s,S四边形AFOE=2s,
∵AD∥BC,
∴∠ADF=∠FCB,
在△ADF和△BCF中,
$\left\{\begin{array}{l}{∠ADF=∠BCF}\\{∠AFD=∠BFC}\\{AF=BF}\end{array}\right.$,
∴△ADF≌△BCF,
∴DF=CF,
∴S△ADF=S△AFC=3s,
∴S△ADF:S四边形AFOE=3:2.
故选D.
点评 本题考查全等三角形的判定和性质、三角形中线的性质、三角形面积问题等知识,解题的关键理解中线把三角形分成面积相等的两部分,异底同高的两个三角形面积比等于底的比,属于中考常考题型.

练习册系列答案
相关题目
8.在“等边三角形、正方形、等腰梯形、平行四边形、矩形、正六边形”中,任取其中一个圆形,恰好是中心对称图形的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
15.下列运算正确的是( )
| A. | ($\frac{a}{b}$)3=$\frac{{a}^{3}}{b}$ | B. | 3a3•2a2=6a6 | C. | 4a6÷2a2=2a3 | D. | (3a2)3=27a6 |
13.某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛,在最近的10次选拔赛中,这两个人的跳远成绩(单位:cm)如图所示,请根据图中信息,解答下列问题:

(1)通过计算,补充完成下面的统计分析表.
(2)请依据对上述统计信息的数据分析,说明这两名运动员的成绩各有什么特点?

(1)通过计算,补充完成下面的统计分析表.
| 运动员 | 平均数 | 众数 | 中位数 | 方差 |
| 甲 | 601.8 | 600 | 600 | 50.56 |
| 乙 | 599.3 | 618 | 595.5 | 284.21 |
 如图,在△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD,AB=12,AC=22,则MD的长为5.
如图,在△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD,AB=12,AC=22,则MD的长为5. 如图,直线a∥b,c∥d,∠1=115°,则∠3=65°.
如图,直线a∥b,c∥d,∠1=115°,则∠3=65°.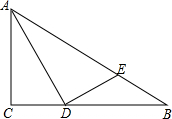 已知,如图,在Rt△ABC中,∠ACB=90°,AB=4,AD是∠BAC的平分线,过点D作DE⊥AD,垂足为点D,交AB于点E,且$\frac{BE}{AB}=\frac{1}{4}$.
已知,如图,在Rt△ABC中,∠ACB=90°,AB=4,AD是∠BAC的平分线,过点D作DE⊥AD,垂足为点D,交AB于点E,且$\frac{BE}{AB}=\frac{1}{4}$.