题目内容
10.不透明的袋子里有5个绿球,2个红球和3个白球,这些球除颜色外无其他差别,从袋子中随机取出1个球,则它是红球的概率为$\frac{1}{5}$.分析 根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率解答即可.
解答 解:∵不透明的袋子里有5个绿球,2个红球和3个白球,这些球除颜色外无其他差别,
∴从袋子中随机取出1个球,则它是红球的概率=$\frac{2}{5+2+3}=\frac{1}{5}$,
故答案为:$\frac{1}{5}$.
点评 本题考查概率的求法与运用,一般方法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.某同学在计算某n边形的内角和时,不小心少输入一个内角,得到和为2005°.则n等于( )
| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
5.若$\frac{1}{x-1}=1$,则$\frac{3}{x-1}-1+x$=( )
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
15.下列运算正确的是( )
| A. | ($\frac{a}{b}$)3=$\frac{{a}^{3}}{b}$ | B. | 3a3•2a2=6a6 | C. | 4a6÷2a2=2a3 | D. | (3a2)3=27a6 |
19.下面计算正确的是( )
| A. | a2+a2=a4 | B. | (-a2)3=(-a)6 | C. | [(-a)2]3=a6 | D. | (a2)3÷a2=a3 |
20.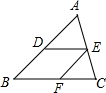 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )
如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )
 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )
如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )| A. | $\frac{AD}{BD}$=$\frac{DE}{BC}$ | B. | $\frac{BF}{BC}$=$\frac{EF}{AD}$ | C. | $\frac{AE}{EC}$=$\frac{BF}{CF}$ | D. | $\frac{EF}{AB}$=$\frac{DE}{BC}$ |
 一块矩形场地,长为101米,宽为70米,从中留出如图所示的宽为1米的小道,其余部分种草,则草坪的面积为6900m2.
一块矩形场地,长为101米,宽为70米,从中留出如图所示的宽为1米的小道,其余部分种草,则草坪的面积为6900m2.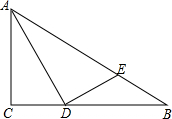 已知,如图,在Rt△ABC中,∠ACB=90°,AB=4,AD是∠BAC的平分线,过点D作DE⊥AD,垂足为点D,交AB于点E,且$\frac{BE}{AB}=\frac{1}{4}$.
已知,如图,在Rt△ABC中,∠ACB=90°,AB=4,AD是∠BAC的平分线,过点D作DE⊥AD,垂足为点D,交AB于点E,且$\frac{BE}{AB}=\frac{1}{4}$.