题目内容
9.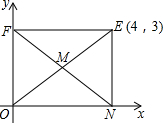 如图,矩形ONEF的对角线交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为(2,1.5).
如图,矩形ONEF的对角线交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为(2,1.5).
分析 先根据四边形ONEF是矩形,由矩形的性质可知点M是对角线OE的中点,根据线段的中点坐标公式即可得出M点的坐标.
解答 解:∵四边形ONEF是矩形,
∴OM=ME,即点M是对角线OE的中点,
∵O(0,0),E(4,3),
∴M($\frac{0+4}{2}$,$\frac{0+3}{2}$),即(2,1.5).
故答案为:(2,1.5).
点评 本题考查了坐标与图形性质,矩形的对角线互相平分的性质,以及线段的中点坐标公式,掌握线段的中点坐标公式:以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$)是解题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
1.某同学在计算某n边形的内角和时,不小心少输入一个内角,得到和为2005°.则n等于( )
| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
19.下面计算正确的是( )
| A. | a2+a2=a4 | B. | (-a2)3=(-a)6 | C. | [(-a)2]3=a6 | D. | (a2)3÷a2=a3 |
 一块矩形场地,长为101米,宽为70米,从中留出如图所示的宽为1米的小道,其余部分种草,则草坪的面积为6900m2.
一块矩形场地,长为101米,宽为70米,从中留出如图所示的宽为1米的小道,其余部分种草,则草坪的面积为6900m2. 【阅读理解】
【阅读理解】 如图,正方形ABCD边长为6,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
如图,正方形ABCD边长为6,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.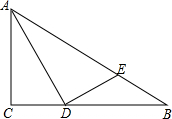 已知,如图,在Rt△ABC中,∠ACB=90°,AB=4,AD是∠BAC的平分线,过点D作DE⊥AD,垂足为点D,交AB于点E,且$\frac{BE}{AB}=\frac{1}{4}$.
已知,如图,在Rt△ABC中,∠ACB=90°,AB=4,AD是∠BAC的平分线,过点D作DE⊥AD,垂足为点D,交AB于点E,且$\frac{BE}{AB}=\frac{1}{4}$.