题目内容
17. 甲、乙两车分别从A、B两地同时出发相向而行,并以各自的速度匀速行驶,甲车与乙车相遇后休息半小时,再按原速度继续前进到达B地;乙车从B地直接到达A地;两车到达各自目的地后即停止.如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
甲、乙两车分别从A、B两地同时出发相向而行,并以各自的速度匀速行驶,甲车与乙车相遇后休息半小时,再按原速度继续前进到达B地;乙车从B地直接到达A地;两车到达各自目的地后即停止.如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.(1)甲车的速度是120,m=1.5;
(2)请分别写出两车在相遇前到B地的距离y(千米)与甲车出发时间x(小时)的函数关系式;
(3)当乙车行驶多少时间时,甲乙两车的距离是280千米.
分析 (1)根据甲车休息半个小时,得到甲车从A地到B地所用时间为3-0.5=2.5小时,用300÷2.5即可得到甲的速度;再用(300-120)除以甲的速度即可得到m的值;
(2)利用待定系数法求一次函数解析式和正比例函数解析式解答;
(3)当0<x<1.5时 (-120x+300)-80x=280,解得x=0.1;因为当x=3时,y乙=240<280,所以x>3,即80x=280,解得x=3.5;综上所述:当乙车行驶了0.1小时或3.5小时,甲、乙两车相距280千米.
解答 解:(1)300÷(3-0.5)=120(千米/小时),m=(300-120)÷120=1.5(小时),
故答案为:120,1.5;
(2)相遇前,自变量x满足:0<x<1.5,
设y甲=kx+b,
把(0,300),(1.5,120)代入得:$\left\{\begin{array}{l}{b=300}\\{1.5k+b=120}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-120}\\{b=300}\end{array}\right.$
∴y甲=-120x+300;
∵乙的速度为:120÷1.5=80(千米/小时),
∴y乙=80x;
(3)当0<x<1.5时 (-120x+300)-80x=280,
解得x=0.1;
因为当x=3时,y乙=240<280,
所以x>3
80x=280
解得x=3.5
综上所述:当乙车行驶了0.1小时或3.5小时,甲、乙两车相距280千米.
点评 本题考查了一次函数的应用,解决本题的关键是利用待定系数法求函数的解析式,在(3)中注意分类讨论思想的应用.

练习册系列答案
相关题目
6.某品牌自行车1月份销售量为100辆,每辆车售价相同.2月份的销售量比1月份增加10%,每辆车的售价比1月份降低了80元.2月份与1月份的销售总额相同,则1月份的售价为( )
| A. | 880元 | B. | 800元 | C. | 720元 | D. | 1080元 |
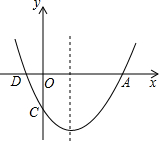 如图,二次函数y=ax2+bx+c的图象与x轴的交点为A、D(A在D的右侧),与y轴的交点为C,且A(4,0).C(0,-3),对称轴是直线x=l.
如图,二次函数y=ax2+bx+c的图象与x轴的交点为A、D(A在D的右侧),与y轴的交点为C,且A(4,0).C(0,-3),对称轴是直线x=l. 如图,点D在△ABC的边BC上,∠C+∠BAD=∠DAC,tan∠BAD=$\frac{4}{7}$,AD=$\sqrt{65}$,CD=13,则线段AC的长为4$\sqrt{13}$.
如图,点D在△ABC的边BC上,∠C+∠BAD=∠DAC,tan∠BAD=$\frac{4}{7}$,AD=$\sqrt{65}$,CD=13,则线段AC的长为4$\sqrt{13}$.