题目内容
5．这样的数称为“正方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是③（填序号）．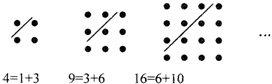
①13=3+10；②25=9+16；③36=15+21；④49=18+31．
分析 任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．由于“正方形数”为两个“三角形数”之和，正方形数可以用代数式表示为：（n+1）2，两个三角形数分别表示为$\frac{1}{2}$n（n+1）和$\frac{1}{2}$（n+1）（n+2），所以由正方形数可以推得n的值，然后求得三角形数的值．
解答 解：显然选项①中13不是“正方形数”；选项②④中等式右侧并不是两个相邻“三角形数”之和．
故答案为：③．
点评 此题考查图形的变化规律，找出图形之间的联系，得出数字之间的运算规律，利用规律解决问题．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
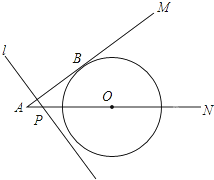如图，⊙O与射线AM相切于点B，圆心O在射线AN上，⊙O半径为6cm，OA=10cm．点P从点A出发，以2cm/秒的速度沿AN方向运动，过P点作直线l垂直AB，当l与⊙O相切时，所用时间是$\frac{5}{4}$或$\frac{35}{4}$秒．
16．下列命题中，正确的是（ ）
| A． | 正方形的对角线不相等 | B． | 菱形的对角线不相等 | ||
| C． | 矩形的对角线不能互相垂直 | D． | 平行四边形的对角线可以互相垂直 |
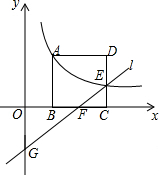如图，正方形ABCD的顶点B，C在x轴的正半轴上，反比例函数y=$\frac{k}{x}$（k≠0）在第一象限的图象经过顶点A（m，2）和CD边上的点E（n，$\frac{2}{3}$），过点E的直线l交x轴于点F，交y轴于点G（0，-2），则点F的坐标是（$\frac{9}{4}$，0）．
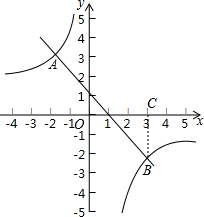如图，在平面直角坐标系xOy中，一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于点A（-2，3），B（3，n）两点．
甲、乙两车分别从A、B两地同时出发相向而行，并以各自的速度匀速行驶，甲车与乙车相遇后休息半小时，再按原速度继续前进到达B地；乙车从B地直接到达A地；两车到达各自目的地后即停止．如图是甲、乙两车和B地的距离y（千米）与甲车出发时间x（小时）的函数图象．
如图，在平面直角坐标系中，抛物线y=a（x-1）2+4与x轴交于点A、B两点，与y轴交于点C，且点B的坐标为（3，0），点P在这条抛物线上，且不与B、C两点重合．过点P作y轴的垂线与射线BC交于点Q，以PQ为边作Rt△PQF，使∠PQF=90°，点F在点Q的下方，且QF=1．设线段PQ的长度为d，点P的横坐标为m．