��Ŀ����
12��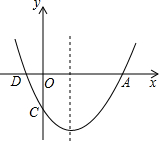 ��ͼ�����κ���y=ax2+bx+c��ͼ����x��Ľ���ΪA��D��A��D���Ҳࣩ����y��Ľ���ΪC����A��4��0����C��0��-3�����Գ�����ֱ��x=l��
��ͼ�����κ���y=ax2+bx+c��ͼ����x��Ľ���ΪA��D��A��D���Ҳࣩ����y��Ľ���ΪC����A��4��0����C��0��-3�����Գ�����ֱ��x=l����1������κ����Ľ���ʽ��
��2����M�ǵ���������������һ���㣬�Һ�����Ϊm�����ı���OCMA�����Ϊs����д��s��m֮��ĺ�����ϵʽ���������mΪ��ֵʱ���ı���OCMA��������
��3�����B��x���ϵĵ㣬P���������ϵĵ㣬�Ƿ���ڵ�P��ʹ����A��B��C��P�ĵ�Ϊ������ı���Ϊƽ���ı��Σ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
���� ��1�������öԳ���ȷ��D�����꣬���轻��ʽy=a��x+2����x-4����Ȼ���C������������a���ɣ�
��2������AC�����ݴ���ϵ�������ֱ��AC�Ľ���ʽΪy=$\frac{3}{4}$x-3����M��MF��x����F����CA��E����M��m��$\frac{3}{8}$m2-$\frac{3}{4}$m-3����E��m��$\frac{3}{4}$m-3������ME=-$\frac{3}{8}$m2+$\frac{3}{2}$m��
����S=S��AOC+S��ACM���ó�S=-$\frac{3}{4}$m2+3m+6�����ݶԳ��᷽�̼������m��ֵ��
��3���֢�AC��ƽ���ı��εı�ʱ�������AC�ij��ȣ��ٸ���ƽ���ı��εĶԱ���������P�������꣬Ȼ�����������߽���ʽ����������������꣬�Ӷ��ý⣻��AC�ǶԽ���ʱ������ƽ���ı��εĶԽ�����ƽ�������P�ģ������꣬Ȼ�����������߽���ʽ����������������꣬�Ӷ��ý⣮
���  �⣻��1����A��4��0�����Գ�����ֱ��x=l��
�⣻��1����A��4��0�����Գ�����ֱ��x=l��
��D��-2��0����
����κ����Ľ���ʽy=a��x+2����x-4����
��C��0��-3����
��-3=-8a��
��a=$\frac{3}{8}$
����κ�������ʽΪ��y=$\frac{3}{8}$��x+2����x-4��=$\frac{3}{8}$x2-$\frac{3}{4}$x-3��
��2����ͼ2������AC��ֱ��AC�Ľ���ʽy=$\frac{3}{4}$x-3����M��MF��x����F����CA��E����M��m��$\frac{3}{8}$m2-$\frac{3}{4}$m-3����E��m��$\frac{3}{4}$m-3������ME=-$\frac{3}{8}$m2+$\frac{3}{2}$m��
��S=S��AOC+S��ACM=$\frac{1}{2}$��3��4+$\frac{1}{2}$��4��EM=6+2��-$\frac{3}{8}$m2+$\frac{3}{2}$m��=-$\frac{3}{4}$m2+3m+6��
��m=-$\frac{3}{2����-\frac{3}{4}��}$=2ʱ��s���
��3�����ڣ�P��2��-3����P��1+$\sqrt{17}$��3����P��1-$\sqrt{17}$��3������ͼ3��
��AC��ƽ���ı��εı�ʱ��
��A��4��0����C��0��-3����
��������P����������3��
��y=3�����3=$\frac{3}{8}$x2-$\frac{3}{4}$x-3��
���x=1��$\sqrt{17}$��
��y=-3�����-3=$\frac{3}{8}$x2-$\frac{3}{4}$x-3��
���x=0��x=2��
��P��������1+$\sqrt{17}$��3����1-$\sqrt{17}$��3����2��-3����
��AC�ǶԽ���ʱ���ߵ�B��x���ϣ�
��AM��PC��
��P��������Ϊ-3��
��ʱ����P������Ϊ��2��-3����
������������P��������1+$\sqrt{17}$��3����1-$\sqrt{17}$��3����2��-3����
���� �����Ƕ��κ����ۺ����ͣ���Ҫ�����˶��κ����ĶԳ��ԣ�����ϵ��������κ�������ʽ������ϵ������һ�κ�������ʽ��ƽ���ı��ζԱ���ȣ��Խ�����ƽ�ֵ����ʣ���3��Ҫ��������ۣ�

 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�| A�� | ���� | B�� | ��ƽ���� | C�� | �� | D�� | ���Ͼ�����ȷ |
��һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ���һ���ڱ���ȵ�ƽ���ı����������Σ�
�۶Խ�����ȵ��ı����Ǿ��Σ� �ܶԽ����ഹֱƽ�ֵ��ı���������
��ȷ���������ǣ�������
| A�� | �٢� | B�� | �ڢ� | C�� | �ۢ� | D�� | �٢� |
| A�� | �ȱ��������ǵ��������� | B�� | ���ab=0����ôa=0��b=0 | ||
| C�� | ���a��0��b��0����ôab��0 | D�� | ȫ�������ε������� |
| A�� | 1��$\sqrt{2}$��$\sqrt{3}$ | B�� | 1��2��3 | C�� | 3��2��1 | D�� | $\sqrt{3}$��$\sqrt{2}$��1 |
 �ס��������ֱ��A��B����ͬʱ����������У����Ը��Ե��ٶ�������ʻ���׳����ҳ���������Ϣ��Сʱ���ٰ�ԭ�ٶȼ���ǰ������B�أ��ҳ���B��ֱ�ӵ���A�أ������������Ŀ�ĵغ�ֹͣ����ͼ�Ǽס���������B�صľ���y��ǧ�ף���׳�����ʱ��x��Сʱ���ĺ���ͼ��
�ס��������ֱ��A��B����ͬʱ����������У����Ը��Ե��ٶ�������ʻ���׳����ҳ���������Ϣ��Сʱ���ٰ�ԭ�ٶȼ���ǰ������B�أ��ҳ���B��ֱ�ӵ���A�أ������������Ŀ�ĵغ�ֹͣ����ͼ�Ǽס���������B�صľ���y��ǧ�ף���׳�����ʱ��x��Сʱ���ĺ���ͼ�� ��5����ȫ��ͬ����������ɵ�����ͼ����ͼ��ʾ�������ĸ���ͼ�ǣ�������
��5����ȫ��ͬ����������ɵ�����ͼ����ͼ��ʾ�������ĸ���ͼ�ǣ�������


