题目内容
10. 如图,在梯形ABCD中,AD∥BC,高AE=12,BD=15,AC=20.求梯形ABCD的面积.
如图,在梯形ABCD中,AD∥BC,高AE=12,BD=15,AC=20.求梯形ABCD的面积.
分析 作BH⊥AD于H.利用勾股定理分别求出EC,DH,易知EC+DH=BC+AD,由此即可解决问题.
解答 解:作BH⊥AD于H.
在Rt△AEC中,∵AE=12,AC=20,
∴CE=$\sqrt{A{C}^{2}-A{E}^{2}}$=$\sqrt{2{0}^{2}-1{2}^{2}}$=16,
在Rt△BDH中,BH=AE=12,BD=15,
∴DH=$\sqrt{1{5}^{2}-1{2}^{2}}$=9,
∴EC+DH=EB+BC+DH=AH+BC+DH=BC+AD=25,
∴S梯形ABCD=$\frac{1}{2}$×25×12=150.
点评 本题考查梯形的面积公式,勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会用转化的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
1.已知xm=2,xn=3,x2m+n=( )
| A. | 12 | B. | 108 | C. | 18 | D. | 36 |
 阅读下列材料:
阅读下列材料: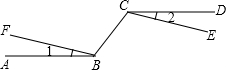 如图,AB∥CD,BF和CE是射线,且∠1=∠2,问BF与CE的位置有什么关系,说明理由.
如图,AB∥CD,BF和CE是射线,且∠1=∠2,问BF与CE的位置有什么关系,说明理由.