Question

4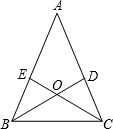．如图，在△ABC中，点D、E分别在边AC、AB上，BD=CE，∠DBC=∠ECB．
（1）说明：其中有几对三角形成轴对称，并指出其对称轴；
（2）连接AO，试判断直线OA与线段BC的关系，并说明理由．

Answer 1

分析 （1）利用轴对称图形的性质即可得出答案；
（2）根据∠DBC=∠ECB得到∠OBC=∠OCB，所以OB=OC，由全等三角形的性质得出AB=AC，OB=OC，说明AO是线段BC的垂直平分线．

解答 解：（1）△ABD和△ACE，△BOE和△COD，△EBC和△DBC，都关于AO所在直线对称，
其对称轴为AO所在直线；

（2）∵∠DBC=∠ECB，
∴OB=OC，
∴点O在线段BC的垂直平分线上，
在△DBC和△ECB中
$\left\{\begin{array}{l}{BD=EC}\\{∠DBC=∠ECB}\\{BC=BC}\end{array}\right.$，
∴△DBC≌△ECB（SAS），
∴∠ABC=∠ACB，
∴AB=AC，∴点A在BC的垂直平分线上，
因此AO是线段BC的垂直平分线．

点评 本题考查了轴对称图形的性质以及线段垂直平分线的性质，正确掌握线段垂直平分线判定方法是解题关键．