题目内容
12.同学们都知道,|5-(-2)|表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离,试探索:(1)|5-(-2)|=7.
(2)同理|x+5|+|x-2|表示数轴上有理数x所对应的点到-5和2所对应的两点距离之和,请你找出所有符合条件的整数x,使得|x+5|+|x-2|=7,这样的整数是5、-4、-3、-2、-1、0、1、2.
(3)由以上探索猜想对于任何有理数x,|x+6|+|x-3|是否有最小值?如果有,写出最小值;如果没有,说明理由.
分析 (1)直接去括号,再按照去绝对值的方法去绝对值就可以了.
(2)要找出x的整数值可以进行分段计算,令x+5=0或x-2=0时,分为3段进行计算,最后确定x的值.
(3)根据绝对值的意义,即可解答.
解答 解:(1)|5-(-2)|=7.
故答案为:7;
(2)令x+5=0或x-2=0时,则x=-5或x=2,
当x<-5时,
∴-(x+5)-(x-2)=7,
-x-5-x+2=7,
x=-5(范围内不成立),
当-5<x<2时,
∴(x+5)-(x-2)=7,
x+5-x+2=7,
7=7,
∴x=-4,-3,-2,-1,0,1,
当x>2时,
∴(x+5)+(x-2)=7,
x+5+x-2=7,
2x=4,
x=2,
x=2(范围内不成立).
∴综上所述,符合条件的整数x有:-5,-4,-3,-2,-1,0,1,2.
故答案为:-5、-4、-3、-2、-1、0、1、2;
(3)有最小值.
当有理数x所对应的点在-6,3之间的线段上的点时,
最小值为9.
点评 本题是一道去绝对值和数轴相联系的综合试题,考查了取绝对值的方法,去绝对值在数轴上的运用.难度较大.去绝对值的关键是确定绝对值里面的数的正负性.

练习册系列答案
相关题目
20.已知点平面内不同的两点A(a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为( )
| A. | -3 | B. | -5 | C. | 1或-3 | D. | 1或-5 |
 如图,B处在A处的南偏西60°方向,C处在A处的南偏东20°方向,C处在B处的正东方向,求∠ACB的度数.
如图,B处在A处的南偏西60°方向,C处在A处的南偏东20°方向,C处在B处的正东方向,求∠ACB的度数. 已知一次函数y=-2x+2
已知一次函数y=-2x+2 如图,△ABC≌△ADE,∠EAC=40°,则∠B=70°.
如图,△ABC≌△ADE,∠EAC=40°,则∠B=70°.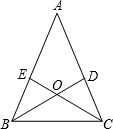 如图,在△ABC中,点D、E分别在边AC、AB上,BD=CE,∠DBC=∠ECB.
如图,在△ABC中,点D、E分别在边AC、AB上,BD=CE,∠DBC=∠ECB.