题目内容
14.某商店经营一种进价为每件15元的日用品.根据经验,如果按每件20元的售价销售,每月能卖出360件;如果按每件25元的售价销售,每月能卖出210件,该商店每月销售件数y(件)是价格x(元/件)的一次函数.(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,才能使每月获得最大利润?每月的最大利润是多少元?
分析 (1)设y与x之间的函数关系式为y=kx+b,可根据题意用待定系数法,求出k,b的值.
(2)利润=单件的利润×销售的数量.然后根据函数的性质来求出利润最大的方案.
解答 解:(1)设y与x之间的函数关系式为y=kx+b,由题意可知:
$\left\{\begin{array}{l}{20k+b=360}\\{25k+b=210}\end{array}\right.$,
解得:k=-30,b=960.
所以y与x之间的函数关系式y=-30x+960.
(2)由(1)可知:y与x的函数关系应该是y=-30x+960
设利润为W,由题意可得
W=(x-15)(-30x+960)=-30x2+1410x-14400.
∵-30<0,
∴当x=-$\frac{1410}{2×(-30)}$=23.5时利润最大,W最大=2167.5,
答:当定价为23.5元时利润最大,最大的利润为2167.5元.
点评 考查了二次函数的应用的知识,二次函数的综合应用题常出现于销售、收费、行程等实际问题当中,利用函数求最值时,主要应用函数的性质.

练习册系列答案
相关题目
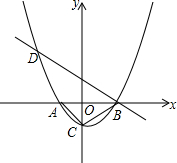 如图,已知抛物线y=m(x+1)(x-2)(m为常数,且m>0)与x轴从左至右依次交于A、B两点,与y轴交于点C,且OA=OC,经过点B的直线与抛物线的另一交点D在第二象限.
如图,已知抛物线y=m(x+1)(x-2)(m为常数,且m>0)与x轴从左至右依次交于A、B两点,与y轴交于点C,且OA=OC,经过点B的直线与抛物线的另一交点D在第二象限. 如图,B处在A处的南偏西60°方向,C处在A处的南偏东20°方向,C处在B处的正东方向,求∠ACB的度数.
如图,B处在A处的南偏西60°方向,C处在A处的南偏东20°方向,C处在B处的正东方向,求∠ACB的度数.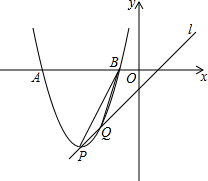 已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1.
已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1. 到直线l1、l2的距离相等的点的轨迹是什么?
到直线l1、l2的距离相等的点的轨迹是什么?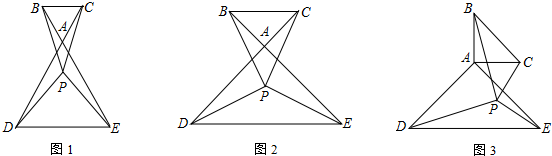
 已知一次函数y=-2x+2
已知一次函数y=-2x+2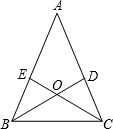 如图,在△ABC中,点D、E分别在边AC、AB上,BD=CE,∠DBC=∠ECB.
如图,在△ABC中,点D、E分别在边AC、AB上,BD=CE,∠DBC=∠ECB.