题目内容
18. 如图,在直角坐标系中,矩形ABCO的边OA在轴上,边OC在轴上,点B的坐标为(6,8),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{24}{5}$,$\frac{32}{5}$).
如图,在直角坐标系中,矩形ABCO的边OA在轴上,边OC在轴上,点B的坐标为(6,8),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{24}{5}$,$\frac{32}{5}$).
分析 由四边形ABCD是矩形,点B的坐标为(6,8),求得BC=OA=6,OC=AB=8,根据等腰三角形的等边对等角,等角对等边,求得点E的坐标,用待定系数法求出直线CD和直线OB 的解析式,联立方程组解出D点的坐标.
解答 解:∵四边形ABCD是矩形,点B的坐标为(6,8),
∴BC=OA=6,OC=AB=8,
∴C(0,8),
∵BD=BE,
∴∠BDE=∠BED,
∵∠OCE=∠BED,∠CDO=∠BDE,
∴∠OCD=∠ODC,
∴OD=OC=8,
∵OB=$\sqrt{O{A}^{2}+A{B}^{2}}$=10,
∴BD=BE=2,
∴E(6,6),
∴直线CE的解析式:y=-$\frac{1}{3}$x+8,
直线OB的解析式:y=$\frac{4}{3}$x,
解$\left\{\begin{array}{l}{y=-\frac{1}{3}x+8}\\{y=\frac{4}{3}x}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{24}{5}}\\{y=\frac{32}{5}}\end{array}\right.$,
∴D($\frac{24}{5}$,$\frac{32}{5}$),
故答案为:($\frac{24}{5}$,$\frac{32}{5}$).
点评 本题考查了矩形的性质,等腰三角形的判定和性质,勾股定理得应用,待定系数法求函数的解析式,解方程组求直线的交点坐标等知识点.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
10.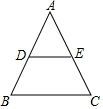 如图,在△ABC中,AB=AC,DE∥BC,则下列结论中,不正确的是( )
如图,在△ABC中,AB=AC,DE∥BC,则下列结论中,不正确的是( )
 如图,在△ABC中,AB=AC,DE∥BC,则下列结论中,不正确的是( )
如图,在△ABC中,AB=AC,DE∥BC,则下列结论中,不正确的是( )| A. | AD=AE | B. | DE=$\frac{1}{2}$EC | C. | ∠ADE=∠C | D. | DB=EC |
7.平面直角坐标系中,若点A(a-2,a)在第二象限,则a的值可能为( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
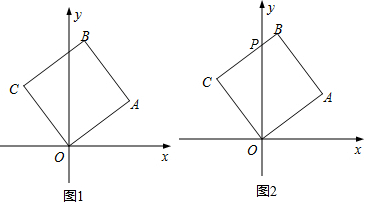
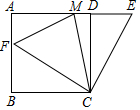 如图,四边形ABCD为正方形,边长为4,E为AD延长线上一点,DE=x(0<x<4),在AE上取一点M,连接CM,将△CME沿CM对折,若点E恰落在线段AB上的点F处,则AM=$\frac{8x}{4+x}$.
如图,四边形ABCD为正方形,边长为4,E为AD延长线上一点,DE=x(0<x<4),在AE上取一点M,连接CM,将△CME沿CM对折,若点E恰落在线段AB上的点F处,则AM=$\frac{8x}{4+x}$.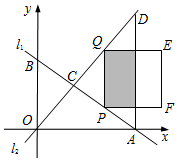 如图,直线l1与坐标轴分别交于点A、B,经过原点的直线l2与AB交于点C,与过点A且平行于y轴的直线交于点D,已知点C(3,$\frac{5}{2}$),且OA=8.在直线AB上取点P,过点P作y轴的平行线,与CD交于点Q,以PQ为边向右作正方形PQEF.设点P的横坐标为t.
如图,直线l1与坐标轴分别交于点A、B,经过原点的直线l2与AB交于点C,与过点A且平行于y轴的直线交于点D,已知点C(3,$\frac{5}{2}$),且OA=8.在直线AB上取点P,过点P作y轴的平行线,与CD交于点Q,以PQ为边向右作正方形PQEF.设点P的横坐标为t.