题目内容
8．解方程：（1）（2x-1）2=（x+3）2
（2）$\frac{3}{4}$x2-2x-$\frac{3}{4}$=0．
分析 （1）两边开方得到2x-1=±（x+3），然后解两个一次方程即可；
（2）先把方程化为3x2-8x-9=10，然后利用因式分解法解方程．
解答 解：（1）2x-1=±（x+3），
所以x1=4，x2=-$\frac{2}{3}$；
（2）3x2-8x-9=10，
（3x+1）（x-3）=0，
3x+1=0或x-3=0，
所以x1=-$\frac{1}{3}$，x2=3．
点评 本题考查了解一元二次方程-因式分解法：因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．
练习册系列答案
优学名师名题系列答案
相关题目
如图，在直角坐标系中，矩形ABCO的边OA在轴上，边OC在轴上，点B的坐标为（6，8），直线CD分别交OB、AB于点D、E，若BD=BE，则点D的坐标为（$\frac{24}{5}$，$\frac{32}{5}$）．
19．下列计算正确的是（ ）
| A． | $\sqrt{3}$+$\sqrt{5}$=$\sqrt{8}$ | B． | $\sqrt{8}$-$\sqrt{3}$=$\sqrt{8-3}$ | C． | $\sqrt{3\frac{2}{3}}$=3$\sqrt{\frac{2}{3}}$ | D． | $\frac{\sqrt{2}}{\sqrt{5}}$=$\frac{\sqrt{10}}{5}$ |
16．已知点A（-1，-5）和点B（2，m），且AB平行于x轴，则B点坐标为（ ）
| A． | （2，-5） | B． | （2，5） | C． | （2，1） | D． | （2，-1） |
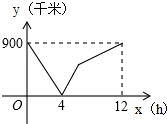一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x小时，两车之间的距离y千米，图中的折线表示y与x之间的函数关系，则出发6小时的时候，甲、乙两车相距450千米．