题目内容
13.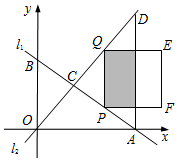 如图,直线l1与坐标轴分别交于点A、B,经过原点的直线l2与AB交于点C,与过点A且平行于y轴的直线交于点D,已知点C(3,$\frac{5}{2}$),且OA=8.在直线AB上取点P,过点P作y轴的平行线,与CD交于点Q,以PQ为边向右作正方形PQEF.设点P的横坐标为t.
如图,直线l1与坐标轴分别交于点A、B,经过原点的直线l2与AB交于点C,与过点A且平行于y轴的直线交于点D,已知点C(3,$\frac{5}{2}$),且OA=8.在直线AB上取点P,过点P作y轴的平行线,与CD交于点Q,以PQ为边向右作正方形PQEF.设点P的横坐标为t.(1)求直线l1的解析式;
(2)当点P在线段AC上时,试求正方形PQEF与△ACD重叠部分(阴影部分)的面积的最大值.
分析 (1)本题需先根据已知条件,设出直线l1的解析式再根据C点的坐标和OA的长,求出k与b的值来,即可求出结果.
(2)先根据题意得出P、Q点的坐标,从而解出t的值,然后再分两种情况进行讨论,分别得出S的最大值,及可求出结果.
解答 解:(1)设直线l1的解析式为y=kx+b,
∵直线l1与直线l2交于点C,
又∵OA=8,
∴把C(3,$\frac{5}{2}$),A(8,0)代入上式得:
$\left\{\begin{array}{l}{8k+b=0}\\{3k+b=\frac{5}{2}}\end{array}\right.$,
解得:b=4,k=-$\frac{1}{2}$,
∴直线l1的解析式为:y=-$\frac{1}{2}$x+4;
(2)点P在线段AC上时,根据题意有:P(t,-$\frac{1}{2}$t+4),Q(t,$\frac{5}{6}$t),
∴PQ=$\frac{5}{6}$t-(-$\frac{1}{2}$t+4)=$\frac{4}{3}$t-4,
当EF在AD上时,t+$\frac{4}{3}$t-4=8,有t=$\frac{36}{7}$,
当3<t≤$\frac{36}{7}$时,S=($\frac{4}{3}$t-4)2,
当t=$\frac{36}{7}$时,S最大=$\frac{400}{49}$,
当 $\frac{36}{7}$≤t≤8时,S=($\frac{4}{3}$t-4)(8-t)=-2(t-$\frac{11}{2}$)2+$\frac{97}{3}$,
当t=$\frac{11}{2}$时,S最大=$\frac{97}{3}$;
所以,S的最大值为 $\frac{97}{3}$;
点评 本题主要考查了一次函数的综合应用,二次函数的应用,解题的关键是掌握待定系数法确定函数解析式,学会构建二次函数解决最值问题.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案| A. | 不变 | B. | 扩大3倍 | C. | 缩小3倍 | D. | 扩大9倍 |
| A. | -1或3 | B. | 2 | C. | 2或3 | D. | -1 |
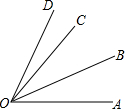 如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )
如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )| A. | 70° | B. | 83° | C. | 68° | D. | 85° |
 如图,在直角坐标系中,矩形ABCO的边OA在轴上,边OC在轴上,点B的坐标为(6,8),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{24}{5}$,$\frac{32}{5}$).
如图,在直角坐标系中,矩形ABCO的边OA在轴上,边OC在轴上,点B的坐标为(6,8),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{24}{5}$,$\frac{32}{5}$).


