题目内容
9.如图1,正方形OABC的顶点O在坐标原点,且OA边和AB边所在直线的解析式分别为:y=$\frac{3}{4}$x和y=-$\frac{4}{3}$x+$\frac{25}{3}$.(1)求A点坐标和正方形OABC的边长;
(2)如图2,现有一动点P从C点出发,沿线段CB向终点B运动.
①当P点位于y轴上时,求△OCP的面积;
②在P点的运动过程中,将△AOP沿它的一边翻折,使得翻折前后的两个三角形组成的四边形为菱形,直接写出满足条件的P点坐标.
(3)若正方形以每秒$\frac{5}{3}$个单位的速度沿射线AO下滑,直至顶点C落在x轴上时停止下滑.设正方形在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围.
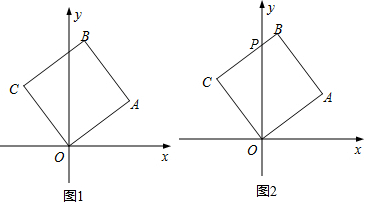
分析 (1)联立方程组求得点A的坐标即可得到结果;
(2)①如图2中,作AM⊥x轴于M,CN⊥x轴于N.利用全等三角形的性质求出点C、B的坐标,求出直线BC的解析式即可解决问题;
②有三种情形:当P与C重合时,△POA沿PA翻折可得菱形,此时P(-3,4);
当P与B重合时,△POA沿PO翻折可得菱形,此时P(1,7);
当P是BC中点时,PO=PA,△POA沿OA翻折可得菱形,此时P(-1,$\frac{11}{2}$),
(3)①当点A运动到点O时,t=3,当0<t≤3时,设O′C′交x轴于点D,根据三角函数的定义tan∠DOO′=$\frac{3}{4}$,即 $\frac{DO′}{OO′}$=$\frac{DO′}{\frac{5}{3}t}$=$\frac{3}{4}$,求得DO′=$\frac{5}{4}$t即可得到S=$\frac{1}{2}$DO′•OO′=$\frac{1}{2}$•$\frac{5}{4}$t•$\frac{5}{3}$t=$\frac{25}{24}$t2;②当点C运动到x轴上时,t=(5×$\frac{4}{3}$)÷$\frac{5}{3}$=4,当3<t≤4时,设A′B′交x轴于点E由于A′O=$\frac{5}{3}$t-5,于是得到A′E=$\frac{3}{4}$A′O=$\frac{5t-15}{4}$即可得到S=$\frac{1}{2}$(A′E+O′D)•A′O′=$\frac{1}{2}$( $\frac{5t-15}{4}$+$\frac{5}{4}$t)•5=$\frac{50t-75}{8}$.
解答 解:(1)联立 $\left\{\begin{array}{l}{y=\frac{3}{4}x}\\{y=-\frac{4}{3}x+\frac{25}{3}}\end{array}\right.$,解得 $\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$,
∴A(4,3),
∴OA=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴正方形OABC的边长为5;
(2)①如图2中,作AM⊥x轴于M,CN⊥x轴于N.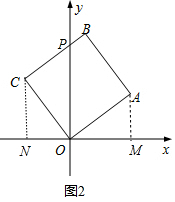
∵CO=OA,∠CON=∠OAM,∠CNO=∠AMO,
∴△CON≌△OAM,
∴ON=AM=3,CN=OM=4,
∴C(-3,4),
∵点O向左平移3个单位,再向上平移4个单位得到C,
∴由A(4,3),可得B(1,7),
∴直线BC的解析式为y=$\frac{3}{4}$x+$\frac{25}{4}$,
∴P(0,$\frac{25}{4}$).
②有三种情形:当P与C重合时,△POA沿PA翻折可得菱形,此时P(-3,4);
当P与B重合时,△POA沿PO翻折可得菱形,此时P(1,7);
当P是BC中点时,PO=PA,△POA沿OA翻折可得菱形,此时P(-1,$\frac{11}{2}$),
综上所述,当P(-3,4)或(1,7)或(-1,$\frac{11}{2}$)时,将△AOP沿它的一边翻折,使得翻折前后的两个三角形组成的四边形为菱形.
∴当k=2或k=4时将△CPQ沿它的一边翻折,使得翻折前后的两个三角形组成的四边形为菱形;
(3)①当点A运动到点O时,t=3,
当0<t≤3时,设O′C′交x轴于点D,
则tan∠DOO′=$\frac{3}{4}$,即 $\frac{DO′}{OO′}$=$\frac{DO′}{\frac{5}{3}t}$=$\frac{3}{4}$,
∴DO′=$\frac{5}{4}$t,
∴S=$\frac{1}{2}$DO′•OO′=$\frac{1}{2}$•$\frac{5}{4}$t•$\frac{5}{3}$t=$\frac{25}{24}$t2,
②当点C运动到x轴上时,t=(5×$\frac{4}{3}$)÷$\frac{5}{3}$=4,
当3<t≤4时,设A′B′交x轴于点E,
∵A′O=$\frac{5}{3}$t-5,
∴A′E=$\frac{3}{4}$A′O=$\frac{5t-15}{4}$,
∴S=$\frac{1}{2}$(A′E+O′D)•A′O′=$\frac{1}{2}$( $\frac{5t-15}{4}$+$\frac{5}{4}$t)•5=$\frac{50t-75}{8}$.
点评 本题考查一次函数综合题、正方形的性质、全等三角形的判定和性质、菱形的判定和性质、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.

 名校课堂系列答案
名校课堂系列答案①了解市面上一次性筷子的卫生情况
②了解我校七年级一班学生升高情况
③了解一批导弹的杀伤范围
④了解全世界网迷少年的性格情况.
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
| A. | 0.5 | B. | 2 | C. | $\sqrt{3}$ | D. | 无法确定 |
| A. | $\sqrt{3}$+$\sqrt{5}$=$\sqrt{8}$ | B. | $\sqrt{8}$-$\sqrt{3}$=$\sqrt{8-3}$ | C. | $\sqrt{3\frac{2}{3}}$=3$\sqrt{\frac{2}{3}}$ | D. | $\frac{\sqrt{2}}{\sqrt{5}}$=$\frac{\sqrt{10}}{5}$ |
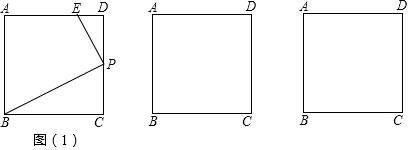
 如图,在直角坐标系中,矩形ABCO的边OA在轴上,边OC在轴上,点B的坐标为(6,8),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{24}{5}$,$\frac{32}{5}$).
如图,在直角坐标系中,矩形ABCO的边OA在轴上,边OC在轴上,点B的坐标为(6,8),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{24}{5}$,$\frac{32}{5}$).