题目内容
10.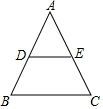 如图,在△ABC中,AB=AC,DE∥BC,则下列结论中,不正确的是( )
如图,在△ABC中,AB=AC,DE∥BC,则下列结论中,不正确的是( )| A. | AD=AE | B. | DE=$\frac{1}{2}$EC | C. | ∠ADE=∠C | D. | DB=EC |
分析 由DE与BC平行,得到三角形ADE与三角形ABC相似,由相似得比例,根据AB=AC,得到AD=AE,进而确定出DB=EC,再由两直线平行同位角相等,以及等腰三角形的底角相等,等量代换得到∠ADE=∠C,而DE不一定为中位线,即DE不一定为BC的一半,即可得到正确选项.
解答 解:∵AB=AC,
∴∠B=∠C,
∵DE∥BC,
∴∠ADE=∠B=∠AED=∠C,
∴AE=AD,
∴∠ADE=∠B,
∵AB=AC,
∴AD=AE,DB=EC,
而DE不一定等于$\frac{1}{2}$EC,
故选B.
点评 此题考查了等腰三角形的判定与性质,以及平行线的性质,熟练掌握等腰三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
5.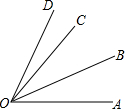 如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )
如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )
 如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )
如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )| A. | 70° | B. | 83° | C. | 68° | D. | 85° |
2.2017年5月13日,国家互联网应急中心NCNCERT发布《关于中点防范Windows操作系统勒索软件攻击的情况公告》,网络安全引起了人们高度重视,下列网络软件的图标中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.下列计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{5}$=$\sqrt{8}$ | B. | $\sqrt{8}$-$\sqrt{3}$=$\sqrt{8-3}$ | C. | $\sqrt{3\frac{2}{3}}$=3$\sqrt{\frac{2}{3}}$ | D. | $\frac{\sqrt{2}}{\sqrt{5}}$=$\frac{\sqrt{10}}{5}$ |
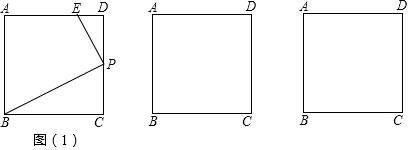
 如图,在直角坐标系中,矩形ABCO的边OA在轴上,边OC在轴上,点B的坐标为(6,8),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{24}{5}$,$\frac{32}{5}$).
如图,在直角坐标系中,矩形ABCO的边OA在轴上,边OC在轴上,点B的坐标为(6,8),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{24}{5}$,$\frac{32}{5}$).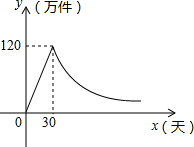 如图,某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图所示),现己知上市30天时,当日销售量为120万件.
如图,某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图所示),现己知上市30天时,当日销售量为120万件.