题目内容
6.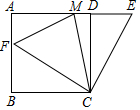 如图,四边形ABCD为正方形,边长为4,E为AD延长线上一点,DE=x(0<x<4),在AE上取一点M,连接CM,将△CME沿CM对折,若点E恰落在线段AB上的点F处,则AM=$\frac{8x}{4+x}$.
如图,四边形ABCD为正方形,边长为4,E为AD延长线上一点,DE=x(0<x<4),在AE上取一点M,连接CM,将△CME沿CM对折,若点E恰落在线段AB上的点F处,则AM=$\frac{8x}{4+x}$.
分析 首先证明Rt△BCF≌Rt△DCE,推出BF=DE=x,设AM=y,在Rt△AFM中,AF=4-x,MF=ME=4-y+x,AM=x,利用勾股定理列出方程求出y即可.
解答  解:∵四边形ABCD是正方形,
解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4,
∵△CMF是由△CME翻折得到,
∴CF=CE,ME=MF,
在Rt△BCF和Rt△DCE中,
$\left\{\begin{array}{l}{BC=CD}\\{CF=CE}\end{array}\right.$,
∴Rt△BCF≌Rt△DCE,
∴BF=DE=x,设AM=y,
在Rt△AFM中,∵AF=4-x,MF=ME=4-y+x,AM=x,
∴(4-x)2+y2=(4-y+x)2,
解得y=$\frac{8x}{x+4}$.
故答案为$\frac{8x}{4+x}$
点评 本题考查正方形的性质、翻折变换、全等三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,学会利用参数构建方程解决问题.

练习册系列答案
相关题目
14.已知二次函数y=ax2-bx+0.5b-a与x轴交于A、B两点,则线段AB的最小值为( )
| A. | 0.5 | B. | 2 | C. | $\sqrt{3}$ | D. | 无法确定 |
11.已知x为任意实数时.函数y=x2+|x-a|+1的最小值为$\frac{7}{4}$,则实数a的值( )
| A. | 1,-$\frac{1}{2}$ | B. | 1,-1 | C. | -1 | D. | $\frac{\sqrt{6}}{2}$,-$\frac{\sqrt{6}}{2}$ |
16.已知点A(-1,-5)和点B(2,m),且AB平行于x轴,则B点坐标为( )
| A. | (2,-5) | B. | (2,5) | C. | (2,1) | D. | (2,-1) |
 如图,在直角坐标系中,矩形ABCO的边OA在轴上,边OC在轴上,点B的坐标为(6,8),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{24}{5}$,$\frac{32}{5}$).
如图,在直角坐标系中,矩形ABCO的边OA在轴上,边OC在轴上,点B的坐标为(6,8),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{24}{5}$,$\frac{32}{5}$).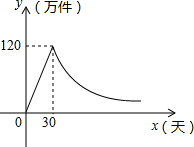 如图,某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图所示),现己知上市30天时,当日销售量为120万件.
如图,某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图所示),现己知上市30天时,当日销售量为120万件.