题目内容
15.若关于x的一元二次方程(m+1)x2-2x+1=0有实数根,则实数m的取值范围是( )| A. | m≥0 | B. | m≤0 | C. | m≠1 | D. | m≤0且m≠-1 |
分析 根据一元二次方程的定义可知m+1≠0,再由方程有实数根可得出△>0,联立关于m的不等式组,求出m的取值范围即可
解答 解:∵关于x的一元二次方程(m+1)x2-2x+1=0有实数根,
∴$\left\{\begin{array}{l}m+1≠0\\△=4-4(m+1)≥0\end{array}\right.$,
解得m≤0且m≠-1.
故选D.
点评 本题考查的是根的判别式,在解答此题时要注意m+1≠0这一隐含条件.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
5. △ABC与?DEFG如图放置,点D,G分别在边AB,AC上,E,F在BC上,已知BE=DE,CF=FG,则∠A的度数为( )
△ABC与?DEFG如图放置,点D,G分别在边AB,AC上,E,F在BC上,已知BE=DE,CF=FG,则∠A的度数为( )
 △ABC与?DEFG如图放置,点D,G分别在边AB,AC上,E,F在BC上,已知BE=DE,CF=FG,则∠A的度数为( )
△ABC与?DEFG如图放置,点D,G分别在边AB,AC上,E,F在BC上,已知BE=DE,CF=FG,则∠A的度数为( )| A. | 80° | B. | 90° | C. | 100° | D. | 110° |
7.已知关于x的一元二次方程x2+$\sqrt{k-1}$x-1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>-7 | B. | k≥-7 | C. | k≥0 | D. | k≥1 |
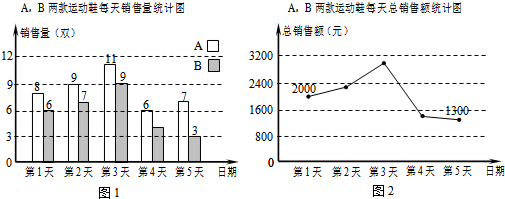
 某校中考模拟试题中有这样一道试题:
某校中考模拟试题中有这样一道试题: