题目内容
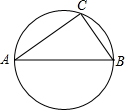 如图,⊙O的面积是25π,△ABC内接于⊙O,a、b、c分别是△ABC的∠A、∠B、∠C的对边(a>b),且a2+b2=c2.sinA、sinB分别是关于x的方程(m+5)x2-(2m-5)x+m-8=0的两根.
如图,⊙O的面积是25π,△ABC内接于⊙O,a、b、c分别是△ABC的∠A、∠B、∠C的对边(a>b),且a2+b2=c2.sinA、sinB分别是关于x的方程(m+5)x2-(2m-5)x+m-8=0的两根.(1)求m的值;
(2)求△ABC的三边长.
考点:圆的综合题
专题:
分析:(1)根据a2+b2=c2可知△ABC是直角三角形,再根据韦达定理得出关于m的方程,求出m的值即可;
(2)根据⊙O的面积是25π求出AB的长,再根据锐角三角函数的定义即可得出a、b的长.
(2)根据⊙O的面积是25π求出AB的长,再根据锐角三角函数的定义即可得出a、b的长.
解答: 解:(1)∵a2+b2=c2,
解:(1)∵a2+b2=c2,
∴△ABC是直角三角形,
∵sinA、sinB分别是关于x的方程(m+5)x2-(2m-5)x+m-8=0的两根,
∴
,
∵(sinA+cosA)2=(sinA)2+(cosA)2+2sinAcosA,即(
)2=1+2×
,整理得,m2-24m+80=0,
∴m1=20,m2=4(舍去);
(2)∵⊙O的面积是25π,
∴25π=(
)2π,
∴AB=10.
将m=20代入原方程得,25x2-35x+12=0,
∵sinA=
=
,sinB=
=
,c=AB=10,
∴a=8,b=6.
 解:(1)∵a2+b2=c2,
解:(1)∵a2+b2=c2,∴△ABC是直角三角形,
∵sinA、sinB分别是关于x的方程(m+5)x2-(2m-5)x+m-8=0的两根,
∴
|
∵(sinA+cosA)2=(sinA)2+(cosA)2+2sinAcosA,即(
| 2m-5 |
| m+5 |
| m+8 |
| m+5 |
∴m1=20,m2=4(舍去);
(2)∵⊙O的面积是25π,
∴25π=(
| AB |
| 2 |
∴AB=10.
将m=20代入原方程得,25x2-35x+12=0,
∵sinA=
| a |
| c |
| 4 |
| 5 |
| b |
| c |
| 3 |
| 5 |
∴a=8,b=6.
点评:本题考查的是圆的综合题,熟知勾股定理及锐角三角函数的定义是解答此题的关键.

练习册系列答案
相关题目
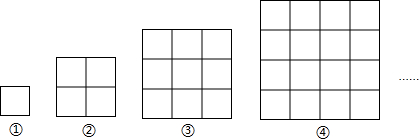
如图,图①由4根火柴围成;图②由12根火柴围成;图③由24根火柴围成;…按此规律,则第⑥个图形由( )根火柴围成.

| A、60 | B、72 | C、84 | D、112 |
 一共要70元
一共要70元 一共要50元.
一共要50元.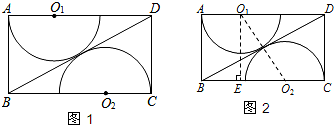 问题:如图1,要在一个矩形木板ABCD上切割、拼接出一个圆形桌面,可在该木板上切割出半径相等的半圆形O1和半圆形O2,其中O1、O2分别是AD、BC上的点,半圆O1分别与AB、BD 相切,半圆O2分别与CD、BD相切.若AB=am,BC=bm,求最终拼接成的圆形桌面的半径(用含a、b的代数式表示).
问题:如图1,要在一个矩形木板ABCD上切割、拼接出一个圆形桌面,可在该木板上切割出半径相等的半圆形O1和半圆形O2,其中O1、O2分别是AD、BC上的点,半圆O1分别与AB、BD 相切,半圆O2分别与CD、BD相切.若AB=am,BC=bm,求最终拼接成的圆形桌面的半径(用含a、b的代数式表示). 如图,梯形ABCD中,AD∥BC,AD<BC,AB=AD,∠BAD=100°,∠BCD=30°,证明:AC=BC.
如图,梯形ABCD中,AD∥BC,AD<BC,AB=AD,∠BAD=100°,∠BCD=30°,证明:AC=BC.