题目内容
 如图,梯形ABCD中,AD∥BC,AD<BC,AB=AD,∠BAD=100°,∠BCD=30°,证明:AC=BC.
如图,梯形ABCD中,AD∥BC,AD<BC,AB=AD,∠BAD=100°,∠BCD=30°,证明:AC=BC.考点:全等三角形的判定与性质,等腰梯形的判定
专题:证明题
分析:作等边△BCE,分别延长BA,CE交于F,连结BD,ED,FD,求出∠ABD=∠ADB=∠DBC=40°,∠ABE=∠DBE=20°,∠BCD=∠ECD=30°,∠BFC=40°,根据SAS证△BCD≌△ECD,推出BD=ED,∠CED=∠CBD=40°,求出四边形FBDE为等腰梯形,推出DF=BE=BC,FE=BD=ED求出∠BFD=∠FDE=∠DFE=
∠DEC=20°,FA=FD=CB,根据SAS证△FAD≌△CBA,推出CA=FD即可.
| 1 |
| 2 |
解答:证明:如图,作等边△BCE,分别延长BA,CE交于F,连结BD,ED,FD,
∵AD∥BC,AD=AB,∠BAD=100°,∠BCD=30°,
∴∠ABD=∠ADB=∠DBC=40°,
∵∠EBC=∠BCE=∠BEC=60°,
∴∠ABE=∠DBE=20°,∠BCD=∠ECD=30°,∠BFC=40°,
在△BCD和△ECD中,
,
∴△BCD≌△ECD(SAS),
∴BD=ED,∠CED=∠CBD=40°,
∴∠BED=∠EBD=∠FBE,
∴FB∥ED
∵∠BFE=∠FBD,
∴四边形FBDE为等腰梯形,
∴DF=BE=BC,FE=BD=ED
∴∠BFD=∠FDE=∠DFE=
∠DEC=20°,
∵∠FAD=∠ABC=80°
∴∠ADF=80°=∠FAD
∴FA=FD=CB
在△FAD与△CBA中,
,
∴△FAD≌△CBA(SAS)
∴CA=FD
∴AC=BC.

∵AD∥BC,AD=AB,∠BAD=100°,∠BCD=30°,
∴∠ABD=∠ADB=∠DBC=40°,
∵∠EBC=∠BCE=∠BEC=60°,
∴∠ABE=∠DBE=20°,∠BCD=∠ECD=30°,∠BFC=40°,
在△BCD和△ECD中,
|
∴△BCD≌△ECD(SAS),
∴BD=ED,∠CED=∠CBD=40°,
∴∠BED=∠EBD=∠FBE,
∴FB∥ED
∵∠BFE=∠FBD,
∴四边形FBDE为等腰梯形,
∴DF=BE=BC,FE=BD=ED
∴∠BFD=∠FDE=∠DFE=
| 1 |
| 2 |
∵∠FAD=∠ABC=80°
∴∠ADF=80°=∠FAD
∴FA=FD=CB
在△FAD与△CBA中,
|
∴△FAD≌△CBA(SAS)
∴CA=FD
∴AC=BC.
点评:本题考查了全等三角形的性质和判定,梯形的性质,等边三角形的性质和判定,平行线的性质的应用,主要考查学生的推理能力,题目比较好,难度偏大.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 如图在△ABC中,∠BAC=90°,AB=AC,CD∥BA,点P是BC上一点,连接AP,过点P作PE⊥AP交CD于E,探究PE与PA的数量关系.
如图在△ABC中,∠BAC=90°,AB=AC,CD∥BA,点P是BC上一点,连接AP,过点P作PE⊥AP交CD于E,探究PE与PA的数量关系.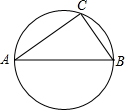 如图,⊙O的面积是25π,△ABC内接于⊙O,a、b、c分别是△ABC的∠A、∠B、∠C的对边(a>b),且a2+b2=c2.sinA、sinB分别是关于x的方程(m+5)x2-(2m-5)x+m-8=0的两根.
如图,⊙O的面积是25π,△ABC内接于⊙O,a、b、c分别是△ABC的∠A、∠B、∠C的对边(a>b),且a2+b2=c2.sinA、sinB分别是关于x的方程(m+5)x2-(2m-5)x+m-8=0的两根.
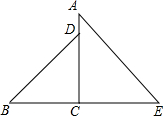 如图所示 AC⊥BE垂足为C,BD=AE,CD=CE,请探索直线BD与直线AE的位置关系.
如图所示 AC⊥BE垂足为C,BD=AE,CD=CE,请探索直线BD与直线AE的位置关系.