题目内容
一个三角形的两边长分别为3和8,且第三边长为奇数,则这个三角形的周长是 .
考点:三角形三边关系,解一元一次不等式组
专题:
分析:可先求出第三边的取值范围,找出其中为奇数的数,即为第三边的长,再将三者相加即可得出周长的值.
解答:解:设第三边长为x.
根据三角形的三边关系,则有8-3<x<8+3,
即5<x<11.
所以x=7或9.
所以周长=3+7+8=18或9+7+8=20.
故答案为18或20.
根据三角形的三边关系,则有8-3<x<8+3,
即5<x<11.
所以x=7或9.
所以周长=3+7+8=18或9+7+8=20.
故答案为18或20.
点评:本题考查了三角形的三边关系,同时能够根据奇数这一条件熟练找到第三边的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法中正确的是( )
| A、3,4,3,5,5,2这组数据的众数是3 | ||||||||
| B、为了解参加运动会的运动员的年龄情况,从中抽了100名运动员的年龄,在这里100名运动员是抽取的一个样本 | ||||||||
C、如果数据x1,x2…xn的平均数是
| ||||||||
| D、一组表据的方差是S2,将这组数据中的每个数据都乘以3,所得的一组新数据的方差是3S2 |
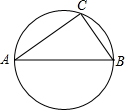 如图,⊙O的面积是25π,△ABC内接于⊙O,a、b、c分别是△ABC的∠A、∠B、∠C的对边(a>b),且a2+b2=c2.sinA、sinB分别是关于x的方程(m+5)x2-(2m-5)x+m-8=0的两根.
如图,⊙O的面积是25π,△ABC内接于⊙O,a、b、c分别是△ABC的∠A、∠B、∠C的对边(a>b),且a2+b2=c2.sinA、sinB分别是关于x的方程(m+5)x2-(2m-5)x+m-8=0的两根.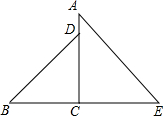 如图所示 AC⊥BE垂足为C,BD=AE,CD=CE,请探索直线BD与直线AE的位置关系.
如图所示 AC⊥BE垂足为C,BD=AE,CD=CE,请探索直线BD与直线AE的位置关系.
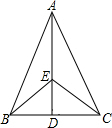 如图所示,已知AB=AC,BE=CE,求证:BD=CD.
如图所示,已知AB=AC,BE=CE,求证:BD=CD.