题目内容
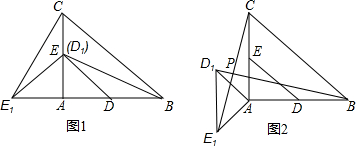
14.在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.

分析 (1)连结OQ,如图1,由PQ∥AB,OP⊥PQ得到OP⊥AB,在Rt△OBP中,利用正切定义可计算出OP=3tan30°=$\sqrt{3}$,然后在Rt△OPQ中利用勾股定理可计算出PQ=$\sqrt{6}$;
(2)连结OQ,如图2,在Rt△OPQ中,根据勾股定理得到PQ=$\sqrt{9-O{P}^{2}}$,则当OP的长最小时,PQ的长最大,根据垂线段最短得到OP⊥BC,则OP=$\frac{1}{2}$OB=$\frac{3}{2}$,所以PQ长的最大值=$\frac{3\sqrt{3}}{2}$.
解答 解:(1)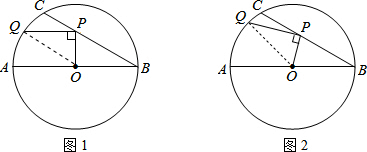 连结OQ,如图1,
连结OQ,如图1,
∵PQ∥AB,OP⊥PQ,
∴OP⊥AB,
在Rt△OBP中,∵tan∠B=$\frac{OP}{OB}$,
∴OP=3tan30°=$\sqrt{3}$,
在Rt△OPQ中,∵OP=$\sqrt{3}$,OQ=3,
∴PQ=$\sqrt{O{Q}^{2}-O{P}^{2}}$=$\sqrt{6}$;
(2)连结OQ,如图2,
在Rt△OPQ中,PQ=$\sqrt{O{Q}^{2}-O{P}^{2}}$=$\sqrt{9-O{P}^{2}}$,
当OP的长最小时,PQ的长最大,
此时OP⊥BC,则OP=$\frac{1}{2}$OB=$\frac{3}{2}$,
∴PQ长的最大值为$\sqrt{9-(\frac{3}{2})^{2}}$=$\frac{3\sqrt{3}}{2}$.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了勾股定理和解直角三角形.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
9.天津地铁1号线、2号线建设总投资153.7亿元,将数字153.7亿元用科学记数法表示为( )
| A. | 153.7×108 | B. | 15.37×108 | C. | 1.537×1010 | D. | 1.537×1011 |
4.下列运算正确的是( )
| A. | (-3mn)2=-6m2n2 | B. | 4x4+2x4+x4=6x4 | C. | (xy)2÷(-xy)=-xy | D. | (a-b)(-a-b)=a2-b2 |
 如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=215°.
如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=215°. 如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,则称点P′是点P关于⊙O的“反演点”.
如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,则称点P′是点P关于⊙O的“反演点”.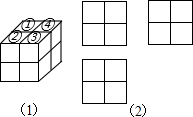 如图,用八个同样大小的小立方体搭成一个大立方体,小明从如图(1)上面的四个小立方体(①②③④)中取走了任意两个后,得到的新几何体的三视图如图(2)所示的概率为$\frac{1}{3}$.
如图,用八个同样大小的小立方体搭成一个大立方体,小明从如图(1)上面的四个小立方体(①②③④)中取走了任意两个后,得到的新几何体的三视图如图(2)所示的概率为$\frac{1}{3}$. 如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且$\widehat{DE}$=$\widehat{BE}$.
如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且$\widehat{DE}$=$\widehat{BE}$.