题目内容
6. 如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且$\widehat{DE}$=$\widehat{BE}$.
如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且$\widehat{DE}$=$\widehat{BE}$.(1)试判断△ABC的形状,并说明理由.
(2)已知半圆的半径为5,BC=12,求sin∠ABD的值.
分析 (1)连结AE,如图,根据圆周角定理,由$\widehat{DE}$=$\widehat{BE}$得∠DAE=∠BAE,由AB为直径得∠AEB=90°,根据等腰三角形的判定方法即可得△ABC为等腰三角形;
(2)由等腰三角形的性质得BE=CE=$\frac{1}{2}$BC=6,再在Rt△ABE中利用勾股定理计算出AE=8,接着由AB为直径得到∠ADB=90°,则可利用面积法计算出BD=$\frac{48}{5}$,然后在Rt△ABD中利用勾股定理计算出AD=$\frac{14}{5}$,再根据正弦的定义求解.
解答 解:(1)△ABC为等腰三角形.理由如下:
连结AE,如图,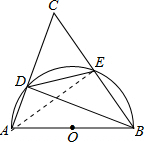
∵$\widehat{DE}$=$\widehat{BE}$,
∴∠DAE=∠BAE,即AE平分∠BAC,
∵AB为直径,
∴∠AEB=90°,
∴AE⊥BC,
∴△ABC为等腰三角形;
(2)∵△ABC为等腰三角形,AE⊥BC,
∴BE=CE=$\frac{1}{2}$BC=$\frac{1}{2}$×12=6,
在Rt△ABE中,∵AB=10,BE=6,
∴AE=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∵AB为直径,
∴∠ADB=90°,
∴$\frac{1}{2}$AE•BC=$\frac{1}{2}$BD•AC,
∴BD=$\frac{8×12}{10}$=$\frac{48}{5}$,
在Rt△ABD中,∵AB=10,BD=$\frac{48}{5}$,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\frac{14}{5}$,
∴sin∠ABD=$\frac{AD}{AB}$=$\frac{\frac{14}{5}}{10}$=$\frac{7}{25}$.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了等腰三角形的判定与性质和勾股定理.

 如图所示的几何体是由一些小正方体组合而成的,则这个几何体的三视图中,面积相等的是( )
如图所示的几何体是由一些小正方体组合而成的,则这个几何体的三视图中,面积相等的是( )| A. | 主视图和左视图 | B. | 主视图和俯视图 | ||
| C. | 左视图和俯视图 | D. | 三种视图面积都相等 |
| A. | -(-3)=3 | B. | (3x)3=9x3 | C. | $\sqrt{4}$=2 | D. | 2-1=$\frac{1}{2}$ |
 如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为( )
如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为( )| A. | 1<k<9 | B. | 2≤k≤34 | C. | 1≤k≤16 | D. | 4≤k<16 |
 如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )
如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )| A. | 6 | B. | 6$\sqrt{3}$ | C. | 9 | D. | 3$\sqrt{3}$ |


 如图,在平面直角坐标系中,抛物线y=mx2-8mx+4m+2(m>0)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2-x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.
如图,在平面直角坐标系中,抛物线y=mx2-8mx+4m+2(m>0)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2-x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q. 如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E.若△BCE的面积为8,则k=16.
如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E.若△BCE的面积为8,则k=16.