题目内容
一辆货车从货场A出发,向西走了1.5千米到达批发部B,接着向东走了2千米到达商场C,又向东走了4.5千米到达超市D,最后回到货场.
(1)用一个单位长度表示1千米,向东为正方向,以货场为原点,画出数轴并在数轴上标明A,B,C,D的位置.
(2)超市D距货场A多远?
(3)货车一共行使了多少千米?
(1)用一个单位长度表示1千米,向东为正方向,以货场为原点,画出数轴并在数轴上标明A,B,C,D的位置.
(2)超市D距货场A多远?
(3)货车一共行使了多少千米?
考点:数轴
专题:
分析:(1)根据题意画出数轴,标出A、B、C、D的位置即可;
(2)根据数轴上两点间的距离公式求解即可;
(3)把货车行驶的路程相加即可.
(2)根据数轴上两点间的距离公式求解即可;
(3)把货车行驶的路程相加即可.
解答:解:(1)如图所示:
 ;
;
(2)∵D点表示5千米,
∴超市D距货场A5千米;
(3)货车一共行驶了:1.5+2+4.5+5=13(千米).
答:货车一共行使了13千米.
 ;
;(2)∵D点表示5千米,
∴超市D距货场A5千米;
(3)货车一共行驶了:1.5+2+4.5+5=13(千米).
答:货车一共行使了13千米.
点评:本题考查的是数轴,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
如果一个多边形的每一个外角都是45°,那么这个多边形的内角和是( )
| A、540° | B、720° |
| C、1080° | D、1260° |
设边长为3的正方形的对角线长为a.下列关于a的四种说法:
①a是无理数; ②a可以用数轴上的一个点来表示;
③a可以写成
(m、n是整数,n≠0)的形式;④3<a<4.
其中,所有正确说法的是( )
①a是无理数; ②a可以用数轴上的一个点来表示;
③a可以写成
| m |
| n |
其中,所有正确说法的是( )
| A、①②③④ | B、①②④ |
| C、①③④ | D、①② |
一张长方形的纸对折,如图所示可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折2次后,可以得3条折痕,那么对折5次可以得到( )条折痕.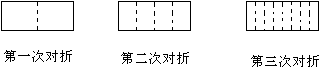

| A、16 | B、15 | C、32 | D、31 |
已知三角形的两边长分别为2cm和7cm,周长是偶数,则这个三角形是( )
| A、不等边三角形 |
| B、等腰三角形 |
| C、等边三角形 |
| D、直角三角形 |