题目内容
一张长方形的纸对折,如图所示可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折2次后,可以得3条折痕,那么对折5次可以得到( )条折痕.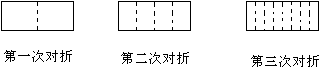

| A、16 | B、15 | C、32 | D、31 |
考点:规律型:图形的变化类
专题:
分析:对前三次对折分析不难发现每对折1次把纸分成的部分是上一次的2倍,折痕比所分成的部分数少1,求出第4次的折痕即可;
再根据对折规律求出对折n次得到的部分数,然后减1即可得到折痕条数.
再根据对折规律求出对折n次得到的部分数,然后减1即可得到折痕条数.
解答:解:由图可知,第1次对折,把纸分成2部分,1条折痕,
第2次对折,把纸分成4部分,3条折痕,
第3次对折,把纸分成8部分,7条折痕,
所以,第4次对折,把纸分成16部分,15条折痕,
…,
依此类推,第n次对折,把纸分成2n部分,2n-1条折痕.
当n=5时,25-1=31,
故选D.
第2次对折,把纸分成4部分,3条折痕,
第3次对折,把纸分成8部分,7条折痕,
所以,第4次对折,把纸分成16部分,15条折痕,
…,
依此类推,第n次对折,把纸分成2n部分,2n-1条折痕.
当n=5时,25-1=31,
故选D.
点评:本题是对图形变化规律的考查,观察得到对折得到的部分数与折痕的关系是解题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案
相关题目
 如图,已知AE⊥BC,AD平分∠BAE,∠ADB=110°,∠CAE=20°.求∠B的度数.
如图,已知AE⊥BC,AD平分∠BAE,∠ADB=110°,∠CAE=20°.求∠B的度数. 在△ABC中,∠C=90°,AD平分∠CAB,交BC与D,过点D作DE⊥AB于E,BC=8cm,BD=5cm,则DE=
在△ABC中,∠C=90°,AD平分∠CAB,交BC与D,过点D作DE⊥AB于E,BC=8cm,BD=5cm,则DE= 已知AD∥EF,∠1=∠2.试说明:AB∥DG.
已知AD∥EF,∠1=∠2.试说明:AB∥DG.