题目内容
已知A、B、C三点，根据下列条件，说明A、B、C三点能否确定一个圆？若能，请求出其半径；若不能，请说明理由．
（1）AB=〔6
+4〕cm，BC=12
cm，AC=〔6
-4〕cm；
（2）AB=AC=10cm，BC=12cm．
（1）AB=〔6
| 3 |
| 3 |
| 3 |
（2）AB=AC=10cm，BC=12cm．
考点：确定圆的条件
专题：
分析：（1）首先通过计算可得两个较短的线段长等于较长的线段长，从而判断出三点在同一条直线上，进而可得A、B、C三点不能确定一个圆；
（2）首先经过计算可得A、B、C三点不在一条直线上，从而得到能确定一个圆，然后再利用勾股定理计算出半径即可．
（2）首先经过计算可得A、B、C三点不在一条直线上，从而得到能确定一个圆，然后再利用勾股定理计算出半径即可．
解答：解：（1）∵6
+4+6
-4=12
，
∴AB+AC=BC，
∴A、B、C三点共线，
∴不能确定一个圆；
（2）∵10+10=20＞12，
∴A、B、C三点不共线，
∴能确定一个圆；
过A作AD⊥BC，连接BO，
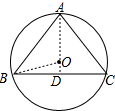
∵BC=12，
∴DB=6，
∵AB=10，
∴AD=
=8，
设OB=x，则DO=8-x，
x2-62=（8-x）2，
解得：x=
．
∴A、B、C三点能确定一个圆，半径为
．
| 3 |
| 3 |
| 3 |
∴AB+AC=BC，
∴A、B、C三点共线，
∴不能确定一个圆；
（2）∵10+10=20＞12，
∴A、B、C三点不共线，
∴能确定一个圆；
过A作AD⊥BC，连接BO，
∵BC=12，
∴DB=6，
∵AB=10，
∴AD=
| 102-62 |
设OB=x，则DO=8-x，
x2-62=（8-x）2，
解得：x=
| 25 |
| 4 |
∴A、B、C三点能确定一个圆，半径为
| 25 |
| 4 |
点评：此题主要考查了确定圆的条件，关键是掌握不在同一直线上的三点确定一个圆．
练习册系列答案
相关题目
当多边形的边数n（n＞3）每减少1时，它的内角和与外角和（ ）
| A、都不变 |
| B、内角和增加180度，外角和不变 |
| C、内角和减少180度，外角和减少180度 |
| D、内角和减少180度，外角和不变 |
已知：如图，∠AOB内有一点P，作点P关于直线OA的对称点P1，再作点P1关于直线OB的对称点P2．试探索∠POP2与∠AOB的大小关系并说明理由．
如图，已知AE⊥BC，AD平分∠BAE，∠ADB=110°，∠CAE=20°．求∠B的度数．