题目内容
17.用简便方法计算(1)-39$\frac{23}{24}$×(-12)
(2)($\frac{2}{3}$-$\frac{1}{12}$-$\frac{1}{15}$)×(-60)
分析 根据乘法分配律,可得答案.
解答 解:(1)原式=(-40+$\frac{1}{24}$)×(-12)=-40×(-12)-$\frac{1}{24}$×12=480-$\frac{1}{2}$=479$\frac{1}{2}$;
(2)原式=$\frac{2}{3}$×(-60)+$\frac{1}{12}$×60+$\frac{1}{15}$×60=-40+5+4=-31.
点评 本题考查了有理数的乘法,利用拆项法得出乘法分配律是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.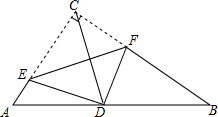 在Rt△ABC中,∠ACB=90°,AC=3,BC=4,翻折∠C,使点C落在边AB的中点D处,折痕为EF(E、F分别在边AC、BC上),则EF的长为( )
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,翻折∠C,使点C落在边AB的中点D处,折痕为EF(E、F分别在边AC、BC上),则EF的长为( )
 在Rt△ABC中,∠ACB=90°,AC=3,BC=4,翻折∠C,使点C落在边AB的中点D处,折痕为EF(E、F分别在边AC、BC上),则EF的长为( )
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,翻折∠C,使点C落在边AB的中点D处,折痕为EF(E、F分别在边AC、BC上),则EF的长为( )| A. | $\frac{5}{2}$ | B. | $\frac{15}{4}$ | C. | $\frac{116}{35}$ | D. | $\frac{125}{48}$ |
2.下列说法中,正确的是( )
| A. | 一组对边相等,另一组对边平行的四边形是平行四边形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 有一组邻边相等的平行四边形是菱形 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
6. 如图所示,下列的图形旋转一周形成左边图形形状的是( )
如图所示,下列的图形旋转一周形成左边图形形状的是( )
 如图所示,下列的图形旋转一周形成左边图形形状的是( )
如图所示,下列的图形旋转一周形成左边图形形状的是( )| A. |  | B. |  | C. |  | D. |  |
7.下列各组向量中,是平行向量的一组是( )
| A. | $\overrightarrow{a}$$+\overrightarrow{b}$与$\frac{1}{2}$$\overrightarrow{a}$$+\overrightarrow{b}$$-\frac{1}{2}$$\overrightarrow{b}$ | B. | $\frac{1}{2}$($\overrightarrow{a}$$-3\overrightarrow{b}$)与$\frac{3}{2}$($\overrightarrow{a}$$-2\overrightarrow{b}$) | C. | 2$\overrightarrow{a}$$+\overrightarrow{b}$与$\overrightarrow{a}$$+\overrightarrow{b}$ | D. | 5$\overrightarrow{a}$$-3\overrightarrow{b}$与$\frac{2}{3}$$\overrightarrow{a}$$-\frac{1}{5}$$\overrightarrow{b}$ |
 观察函数y=x2-3x+2的图象,回答下列问题:
观察函数y=x2-3x+2的图象,回答下列问题: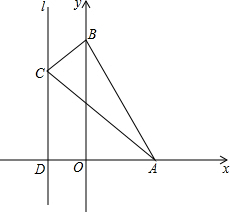 在平面直角坐标系xOy中,点A的坐标为(2,0),点B的坐标为(0,4),直线l经过(-1,0)并且与x轴垂直于点D,请你在直线l上找一点C,使△ABC为直角三角形,并求出点C的坐标.
在平面直角坐标系xOy中,点A的坐标为(2,0),点B的坐标为(0,4),直线l经过(-1,0)并且与x轴垂直于点D,请你在直线l上找一点C,使△ABC为直角三角形,并求出点C的坐标.