题目内容
8.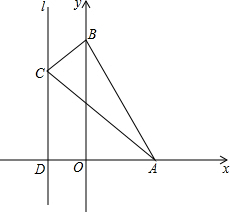 在平面直角坐标系xOy中,点A的坐标为(2,0),点B的坐标为(0,4),直线l经过(-1,0)并且与x轴垂直于点D,请你在直线l上找一点C,使△ABC为直角三角形,并求出点C的坐标.
在平面直角坐标系xOy中,点A的坐标为(2,0),点B的坐标为(0,4),直线l经过(-1,0)并且与x轴垂直于点D,请你在直线l上找一点C,使△ABC为直角三角形,并求出点C的坐标.
分析 设点C的坐标为(-1,b),根据点的坐标的性质用b表示出AB2、AC2、BC2,分∠ABC=90°、∠BAC=90°和∠ACB=90°,根据勾股定理列出方程,解方程即可得到答案.
解答 解:设点C的坐标为(-1,b),
AB2=22+42=20,
AC2=32+b2,
BC2=(4-b)2+12,
当∠ABC=90°时,(4-b)2+12+20=32+b2,
解得,b=$\frac{7}{2}$;
当∠BAC=90°时,(4-b)2+12=20+32+b2,
解得,b=-$\frac{3}{2}$;
当∠ACB=90°时,(4-b)2+12+32+b2=20,
解得b1=1,b2=3,
∴△ABC为直角三角形时,点C的坐标为(-1,$\frac{7}{2}$),(-1,-$\frac{3}{2}$),(-1,1),(-1,3).
点评 本题考查的是一次函数知识的综合运用,掌握勾股定理、正确运用分情况讨论思想是解题的关键.

练习册系列答案
相关题目
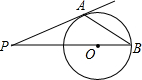 如图,PA切⊙O于A,PO交⊙O于B,若∠P=35°,则∠PBA=27.5°.
如图,PA切⊙O于A,PO交⊙O于B,若∠P=35°,则∠PBA=27.5°.