题目内容
5.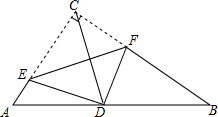 在Rt△ABC中,∠ACB=90°,AC=3,BC=4,翻折∠C,使点C落在边AB的中点D处,折痕为EF(E、F分别在边AC、BC上),则EF的长为( )
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,翻折∠C,使点C落在边AB的中点D处,折痕为EF(E、F分别在边AC、BC上),则EF的长为( )| A. | $\frac{5}{2}$ | B. | $\frac{15}{4}$ | C. | $\frac{116}{35}$ | D. | $\frac{125}{48}$ |
分析 作CH⊥AB于H,根据勾股定理求出AB的长,根据三角形面积公式求出CH,根据直角三角形的性质求出CG,证明△ECF∽△BCA,得到比例式,计算即可.
解答 解:作CH⊥AB于H,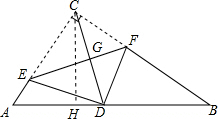
∵∠ACB=90°,AC=3,BC=4,
∴AB=5,CH=$\frac{12}{5}$,
∵∠ACB=90°,AD=DB,
∴CD=$\frac{1}{2}$AB=$\frac{5}{2}$,
∴CG=$\frac{5}{4}$,
∵∠ECG+∠CEG=90°,∠ECG+∠GCF=90°,
∵∠GCF=∠CEG,
∵CD=BD,
∴∠CBD=∠CEG,
∴△ECF∽△BCA,
∴$\frac{EF}{AB}$=$\frac{CG}{CH}$,即$\frac{EF}{5}$=$\frac{\frac{5}{4}}{\frac{12}{5}}$,
解得EF=$\frac{125}{48}$,
故选:D.
点评 本题考查的是翻折变换的性质,找准翻折变换中的对应边和对应角、正确运用相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
15.下列运算正确的是( )
| A. | 2a2-a2=2 | B. | a3+a3=a6 | C. | (a3)2=a6 | D. | a8÷a4=a2 |
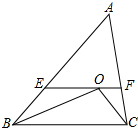 如图,△ABC中,∠B与∠C的平分线交于点O,过O作EF∥BC交AB、AC于E、F,若△ABC的周长比△AEF的周长大12cm,O到AB的距离为3cm,△OBC的面积18cm2.
如图,△ABC中,∠B与∠C的平分线交于点O,过O作EF∥BC交AB、AC于E、F,若△ABC的周长比△AEF的周长大12cm,O到AB的距离为3cm,△OBC的面积18cm2.