题目内容
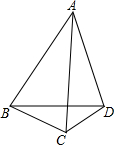 如图,∠ABD=∠ACD=60°,∠ADB=90°-
如图,∠ABD=∠ACD=60°,∠ADB=90°-| 1 |
| 2 |
考点:全等三角形的判定与性质,等腰三角形的判定
专题:
分析:延长CD至E,使DE=BD,连接AE,易证∠ADE=∠ADB,即可证明△ABD≌△AED,可得∠ABD=∠E,AB=AE,即可求得AC=AE,可得AB=AC,即可解题.
解答:解:延长CD至E,使DE=BD,连接AE,
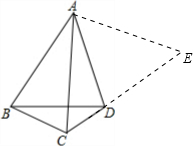
∵∠ADB=90°-
∠BDC,
∴∠BDC=180°-2∠ADB,
∴∠ADE=180°-∠BDC-∠ADB
=180°-(180°-2∠ADB)-∠ADB
=∠ADB,
∵在△ABD和△AED中,
,
∴△ABD≌△AED,(SAS)
∴∠ABD=∠E,AB=AE,
∵∠ABD=60°,∴∠E=60°,
∵∠ACD=60°,∴∠ACD=∠E,
∴AC=AE,
∴AB=AC,
∴△ABC是等腰三角形.

∵∠ADB=90°-
| 1 |
| 2 |
∴∠BDC=180°-2∠ADB,
∴∠ADE=180°-∠BDC-∠ADB
=180°-(180°-2∠ADB)-∠ADB
=∠ADB,
∵在△ABD和△AED中,
|
∴△ABD≌△AED,(SAS)
∴∠ABD=∠E,AB=AE,
∵∠ABD=60°,∴∠E=60°,
∵∠ACD=60°,∴∠ACD=∠E,
∴AC=AE,
∴AB=AC,
∴△ABC是等腰三角形.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ABD≌△AED是解题的关键.

练习册系列答案
相关题目
在
,
,
,
四个数中,无理数共有( )
| 4 |
| 3 | -9 |
| π |
| 3 |
| 355 |
| 113 |
| A、1个 | B、2个 | C、3个 | D、4个 |
已知x=1+2m,y=1+
,则y=( )
| 1 |
| 2m |
| A、x | ||
B、
| ||
C、
| ||
D、
|
 有理数a,b在数轴上的位置如图所示,则b-a
有理数a,b在数轴上的位置如图所示,则b-a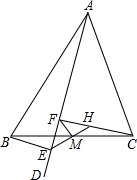 如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,延长CH交AD于F,则下列结论中:(1)M是BC的中点.(2)CF⊥AD.(3)FM⊥BC.(4)FM=
如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,延长CH交AD于F,则下列结论中:(1)M是BC的中点.(2)CF⊥AD.(3)FM⊥BC.(4)FM=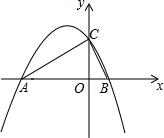 如图,设二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y轴交于C点,若AC=8,BC=6,∠ACB=90°,求这个二次函数的解析式.
如图,设二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y轴交于C点,若AC=8,BC=6,∠ACB=90°,求这个二次函数的解析式.