题目内容
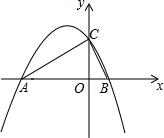 如图,设二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y轴交于C点,若AC=8,BC=6,∠ACB=90°,求这个二次函数的解析式.
如图,设二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y轴交于C点,若AC=8,BC=6,∠ACB=90°,求这个二次函数的解析式.考点:待定系数法求二次函数解析式
专题:
分析:利用勾股定理得出AB的长,再利用三角形面积求出CO的长,进而求出A,B,C点坐标,进而求出出函数解析式.
解答:解:∵AC=8,BC=6,∠ACB=90°,
∴AB=
=10,
∴6×8=10•CO,
解得:CO=4.8,
∴C(0,4.8),
∴BO=
=3.6,AO=10-3.6=6.4,
∴A(-6.4,0),B(3.6,0),
∴设二次函数解析式为:y=a(x+6.4)(x-3.6),
∵过C(0,4.8),
∴4.8=a×6.4×(-3.6),
解得:a=-
,
∴二次函数解析式为y=-
(x+
)(x-
).
∴AB=
| AC2+BC2 |
∴6×8=10•CO,
解得:CO=4.8,
∴C(0,4.8),
∴BO=
| CB2-CO2 |
∴A(-6.4,0),B(3.6,0),
∴设二次函数解析式为:y=a(x+6.4)(x-3.6),
∵过C(0,4.8),
∴4.8=a×6.4×(-3.6),
解得:a=-
| 5 |
| 24 |
∴二次函数解析式为y=-
| 5 |
| 24 |
| 5 |
| 32 |
| 5 |
| 18 |
点评:此题主要考查了勾股定理以及抛物线与x轴交点问题,得出A,B,C点坐标是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列多项式中是二次二项式的是( )
| A、3x2+2x+1 |
| B、-x4+9 |
| C、x2-2x |
| D、x3-3x2+4 |
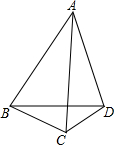 如图,∠ABD=∠ACD=60°,∠ADB=90°-
如图,∠ABD=∠ACD=60°,∠ADB=90°-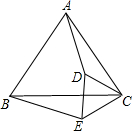 如图所示,已知:△ABC和△CDE都是等边三角形,求证:AD=BE.
如图所示,已知:△ABC和△CDE都是等边三角形,求证:AD=BE. 如图所示,已知O是直线AB上的一点,∠1=40°,OD平分∠BOC,则∠2=
如图所示,已知O是直线AB上的一点,∠1=40°,OD平分∠BOC,则∠2=