题目内容
12.已知函数y=mx2-6x+1(m是常数).(1)当该函数的图象与x轴有两个公共点时,求m的取值范围.并求m为最大整数时,方程mx2-6x+1=0(m是常数)的两根;
(2)若该函数的图象与x轴只有一个公共点,求m的值.
分析 (1)根据函数的图象与x轴有两个公共点,则关于x的一元二次方程mx2-6x+1=0有两个不相等的实数根,根据根的判别式求出m的取值范围;再解方程即可求出方程的两根;
(2)分m=0和m≠0两种情况进行讨论.
解答 解:(1)∵已知函数y=mx2-6x+1(m是常数),当该函数的图象与x轴有两个公共点,
∴令y=mx2-6x+1=0,
∴关于x的一元二次方程mx2-6x+1=0有两个不相等的实数根,
∴△=36-4m>0且m≠0,即m<9且m≠0,
∴m的最大整数为8,则方程为8x2-6x+1=0,
∴解方程得x1=$\frac{1}{2}$,x2=$\frac{1}{4}$;
(2)当m=0时,函数y=-6x+1,一次函数图象与x轴只有一个交点,
当m≠0时,
∵该函数的图象与x轴只有一个公共点,
∴令y=mx2-6x+1=0,由(1)可知△=36-4m,
∴36-4m=0,即m=9,
综上m的值为0或9.
点评 本题主要考查了抛物线与x轴的交点以及二次函数的最值,解题的关键是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
3.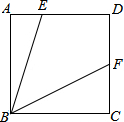 如图,已知正方形ABCD中,E在AD边上,F在CD边上,且∠EBF=45°,若AE=2,CF=3,则AB长( )
如图,已知正方形ABCD中,E在AD边上,F在CD边上,且∠EBF=45°,若AE=2,CF=3,则AB长( )
 如图,已知正方形ABCD中,E在AD边上,F在CD边上,且∠EBF=45°,若AE=2,CF=3,则AB长( )
如图,已知正方形ABCD中,E在AD边上,F在CD边上,且∠EBF=45°,若AE=2,CF=3,则AB长( )| A. | 5.5 | B. | 6 | C. | 6.5 | D. | 7 |
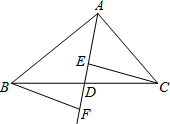 如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E、F,连接CE、BF.添加一个条件DE=DF,使得△BDF≌△CDE,依据是SAS.
如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E、F,连接CE、BF.添加一个条件DE=DF,使得△BDF≌△CDE,依据是SAS.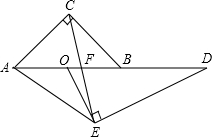 在等腰Rt△ABC中,∠ACB=90°,O是AB的中点,D在AB的延长线上,E在AD下方且∠OED=90°,∠OAE=∠OEA,CE交AD于F.
在等腰Rt△ABC中,∠ACB=90°,O是AB的中点,D在AB的延长线上,E在AD下方且∠OED=90°,∠OAE=∠OEA,CE交AD于F.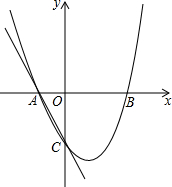 如图,一次函数y=x2-x-2的图象交x轴于A,B两点,交y轴于C,点M在第一象限的抛物线上,CM交x轴于点P,且PA=PC,求点M的坐标.
如图,一次函数y=x2-x-2的图象交x轴于A,B两点,交y轴于C,点M在第一象限的抛物线上,CM交x轴于点P,且PA=PC,求点M的坐标.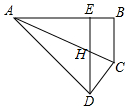 如图,将Rt△ABC沿斜边AC所在直线翻折后点B落到点D,过点D作DE⊥AB,垂足为E,如果AE=3EB,EB=7,那么BC=4$\sqrt{7}$.
如图,将Rt△ABC沿斜边AC所在直线翻折后点B落到点D,过点D作DE⊥AB,垂足为E,如果AE=3EB,EB=7,那么BC=4$\sqrt{7}$.