题目内容
1.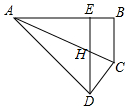 如图,将Rt△ABC沿斜边AC所在直线翻折后点B落到点D,过点D作DE⊥AB,垂足为E,如果AE=3EB,EB=7,那么BC=4$\sqrt{7}$.
如图,将Rt△ABC沿斜边AC所在直线翻折后点B落到点D,过点D作DE⊥AB,垂足为E,如果AE=3EB,EB=7,那么BC=4$\sqrt{7}$.
分析 根据相似三角形的判定和性质、以及勾股定理解答即可.
解答 解:∵DE⊥AB,∠B=90°,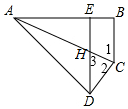
∴DE∥BC,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∴DH=DC,
∵DE∥BC,
∴△AEH∽△ABC,
∴$\frac{AE}{AB}$=$\frac{EH}{BC}$=$\frac{3}{4}$,
设EH=3x,BC=DC=DH=4x,
∴DE=7x,
∵AE=3EB,EB=7,
∴AE=21,
∵AD=AB=AE+BE=7+21=28,
在Rt△ADE中,DE=$\sqrt{A{D}^{2}-A{E}^{2}}=\sqrt{2{8}^{2}-2{1}^{2}}=7\sqrt{7}$,
∴7x=7$\sqrt{7}$,
∴x=$\sqrt{7}$,
∴BC=4$\sqrt{7}$.
故答案为:4$\sqrt{7}$.
点评 此题考查相似三角形的判定和性质,证明DH=DC是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.投掷一枚均匀的骰子,掷出的点数是3的倍数的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
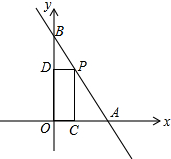 如图,一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A、B重合),过点P分别作OA和OB的垂线,垂足分别为C、D.
如图,一次函数y=-$\sqrt{3}$x+2$\sqrt{3}$的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A、B重合),过点P分别作OA和OB的垂线,垂足分别为C、D. 如图所示,已知四边形ABCD和点O,画出四边形ABCD绕点O顺时针旋转90°后的图形.
如图所示,已知四边形ABCD和点O,画出四边形ABCD绕点O顺时针旋转90°后的图形.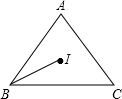 如图,在△ABC中,AB=AC=10,BC=12,I为△ABC的内心.
如图,在△ABC中,AB=AC=10,BC=12,I为△ABC的内心. 一次函数y=kx+b的图象如图,则当0≤x≤1时,y的范围是-2≤y<0.
一次函数y=kx+b的图象如图,则当0≤x≤1时,y的范围是-2≤y<0.