题目内容
16.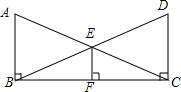 如图,已知AB⊥BC,DC⊥BC,AC与BD相交于点E,过E作EF⊥BC于点F,且AC=BD.求证:
如图,已知AB⊥BC,DC⊥BC,AC与BD相交于点E,过E作EF⊥BC于点F,且AC=BD.求证:(1)△ABC≌△DCB;
(2)EF是∠BEC的角平分线.
分析 (!)由HL定理直接推出结论;
(2)由Rt△ABC≌Rt△DCB,得到EB=EC,由等腰三角形的性质定理即可推出结论.
解答 (1)证明:在Rt△ABC和Rt△DCB中,
$\left\{\begin{array}{l}{AC=BD}\\{BC=CB}\end{array}\right.$,
∴Rt△ABC≌Rt△DCB(HL);
(2)∵Rt△ABC≌Rt△DCB,
∴∠EBC=∠ECB,
∴EB=EC,
∵EF⊥BC.
∴EF是∠BEC的角平分线.
点评 本题主要考查了直角三角形全等的判定定理及其性质,等腰三角形的性质,熟练等腰三角形的性质“三线合一”解决问题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
6.多项式1-4t+4t2可以分解为( )
| A. | (4t-1)2 | B. | -(2t-1)2 | C. | (2t-1)2 | D. | (1-4t)2 |
7.下列各视图中,能组成一个立体图形的三种视图的是( )


| A. | ①②⑥ | B. | ①③⑤ | C. | ②③⑤ | D. | ②③④ |
4.抛物线y=x2-2x+c与y轴的交点为(0,-3),则下列说法错误的是( )
| A. | 抛物线开口向上 | B. | 抛物线的对称轴是x=1 | ||
| C. | 当x=1时,y的最大值为-4 | D. | c=-3 |
11.若多项式4x2-kxy+y2是完全平方式,则k的值是( )
| A. | 4 | B. | ±4 | C. | -4 | D. | 2 |
8.已知点(-4,y1),(2,y2)都在直线y=-$\frac{1}{2}$x-m上,则y1、y2大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
5.计算(-2)2015+3×(-2)2014的结果是( )
| A. | -22014 | B. | 22014 | C. | 1 | D. | -22015 |
6. 长方形纸片ABCD中,E为AD边上一点,将纸片沿BE折叠后,点A落在CD边上F点,若∠CBF=∠EBF,则∠DEF的度数为( )
长方形纸片ABCD中,E为AD边上一点,将纸片沿BE折叠后,点A落在CD边上F点,若∠CBF=∠EBF,则∠DEF的度数为( )
 长方形纸片ABCD中,E为AD边上一点,将纸片沿BE折叠后,点A落在CD边上F点,若∠CBF=∠EBF,则∠DEF的度数为( )
长方形纸片ABCD中,E为AD边上一点,将纸片沿BE折叠后,点A落在CD边上F点,若∠CBF=∠EBF,则∠DEF的度数为( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
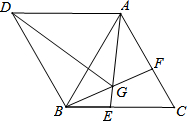 如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.