题目内容
4.抛物线y=x2-2x+c与y轴的交点为(0,-3),则下列说法错误的是( )| A. | 抛物线开口向上 | B. | 抛物线的对称轴是x=1 | ||
| C. | 当x=1时,y的最大值为-4 | D. | c=-3 |
分析 先把(0,-3)代入y=x2-2x+c中求出c的值,再把解析式配成顶点式,然后根据二次函数的性质对各选项进行判断.
解答 解:把(0,-3)代入y=x2-2x+c得c=-3,则y=x2-2x-3=(x-1)2-4,
所以抛物线开口向上,对称轴为直线x=1,当x=1时,y有最小值-4.
故选C.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.本题的关键是确定抛物线的顶点式.

练习册系列答案
相关题目
19.下列计算结果为负数的是( )
| A. | -(-2)3 | B. | -24 | C. | (-1)×(-3)5 | D. | 23×(-2)6 |
9.已知:分式$\frac{{x}^{2}+2x-3}{|x|-1}$的值为零,分式$\frac{{y}^{2}-3}{{y}^{2}+y-2}$无意义,则x+y的值是( )
| A. | -5或-2 | B. | -1或-4 | C. | 1或4 | D. | 5或2 |
13.下列运用平方差公式进行计算,错误的是( )
| A. | (a+b)(a-b)=a2-b2 | B. | (x+1)(x-1)=x2-1 | ||
| C. | (-3x+2)(-3x-2)=9x2-4 | D. | (2x+1)(2x-1)=2x2-1 |
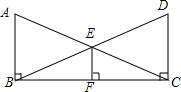 如图,已知AB⊥BC,DC⊥BC,AC与BD相交于点E,过E作EF⊥BC于点F,且AC=BD.求证:
如图,已知AB⊥BC,DC⊥BC,AC与BD相交于点E,过E作EF⊥BC于点F,且AC=BD.求证: