题目内容
1.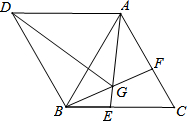 如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.(1)求∠AGF的度数;
(2)连接DG,若AG=3、BG=2,求DG的长.
分析 (1)根据等边三角形的性质得到AB=BC,∠ABC=∠C=60°,再根据三角形全等的判定方法可证得△ABE≌△BCF,则∠BAE=∠FBC,利用三角形外角性质得∠BGE=∠ABG+∠BAE,则∠BGE=∠ABG+∠FBC=∠ABC=60°,然后根据对顶角相等即可得到结论;
(2)延长GE至点H,使GH=GB,由于∠BGE=60°,根据等边三角形的判定得到△BGH为等边三角形,然后根据等边三角形的性质得到BG=BH=GH,∠GBH=60°,且AB=BD,∠ABD=60°,易得∠ABH=∠DBG,根据三角形全等的判定方法可证得△DBG≌△ABH(SAS),则DG=AH,即可得到DG=AG+BG.
解答 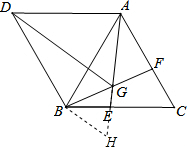 (1)解:∵△ABC是等边三角形,
(1)解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°,
∵在△ABE和△BCF中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠C}\\{BE=CF}\end{array}\right.$,
∴△ABE≌△BCF(SAS),
∴∠BAE=∠FBC,
∵∠BGE=∠ABG+∠BAE=∠ABG+∠FBC=∠ABC=60°,
∴∠AGF=∠BGE=60°;
(2)证明:延长GE至点H,使GH=GB,如图,
∵∠BGE=60°,
∴△BGH为等边三角形,
∴BG=BH=GH,∠GBH=60°,
∵△ABD是等边三角形,
∴AB=BD,∠ABD=60°,
∵∠ABH=∠GBH+∠ABG,∠DBG=∠ABD+∠ABG,
∴∠ABH=∠DBG,
∵在△DBG和△ABH中,
$\left\{\begin{array}{l}{DB=AB}\\{∠DBG=∠ABH}\\{BG=BH}\end{array}\right.$,
∴△DBG≌△ABH(SAS),
∴DG=AH,
而AH=AG+GH,
∴DG=AG+BG,
∵AG=3、BG=2,
∴DG=5.
点评 本题考查了全等三角形的判定与性质,等边三角形的性质和判定,三角形外角的性质,正确的作出辅助线是解题的关键.

 如图,?ABCD中,EF∥AB,DE:EA=1:2,EF=4,则CD的长为( )
如图,?ABCD中,EF∥AB,DE:EA=1:2,EF=4,则CD的长为( )| A. | $\frac{4}{3}$ | B. | 8 | C. | 12 | D. | 16 |
| A. | -5或-2 | B. | -1或-4 | C. | 1或4 | D. | 5或2 |
 如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )| A. | AC=BC+CE | B. | ∠A=∠2 | C. | △ABC≌△CED | D. | ∠A与∠D互余 |
| A. | (a+b)(a-b)=a2-b2 | B. | (x+1)(x-1)=x2-1 | ||
| C. | (-3x+2)(-3x-2)=9x2-4 | D. | (2x+1)(2x-1)=2x2-1 |
| A. | (-2,0) | B. | (2,0) | C. | (0,-2) | D. | (0,2) |
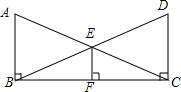 如图,已知AB⊥BC,DC⊥BC,AC与BD相交于点E,过E作EF⊥BC于点F,且AC=BD.求证:
如图,已知AB⊥BC,DC⊥BC,AC与BD相交于点E,过E作EF⊥BC于点F,且AC=BD.求证: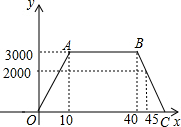 (1)请仔细观察并根据下列函数图,结合生活实际,编一个故事,使故事情境中出现的一对变量x,y满足图示的函数关系式,要求:
(1)请仔细观察并根据下列函数图,结合生活实际,编一个故事,使故事情境中出现的一对变量x,y满足图示的函数关系式,要求: